矩阵理论与计算复习章
1. 代数与矩阵运算
1.1 向量范数与矩阵范数
1.1.1 向量范数
1.1.2 矩阵范数
向量范数 与 矩阵范数 相容 :
$||Ax|| \leq ||A|| ||x||$
如:矩阵范数$m_1$与向量范数$l_1$相容 ; 矩阵范数$m_2$与向量范数$l_2$相容
对于一个向量范数,一定能找到一个与之相容的矩阵范数:
$||A|| = \underset{||x||=1}{\max} ||Ax||$
两种矩阵范数:
- 非从属矩阵范数:$m_1$, $m_2$等
- 算子范数:由向量范数诱导得到的矩阵范数
- 极大的列和范数:$||A||{1} = \underset{1 \leq j \leq n}{\max} \sum{i=1}^{m} |a_{ij}|$ 所有列和里面最大的
- 谱范数:$||A||_2 = (\lambda ^{\frac{1}{2}} (A^HA))$ (取$A^HA$的最大的特征值)
- 极大的行和范数:$||A||{\infty} = \underset{1 \leq i \leq m}{\max} \sum{j=1}^{n} |a_{ij}|$
两者的区别:非从属矩阵范数有$||I|| \geq 1$ ; 而算子范数 $||I|| = 1$
例题
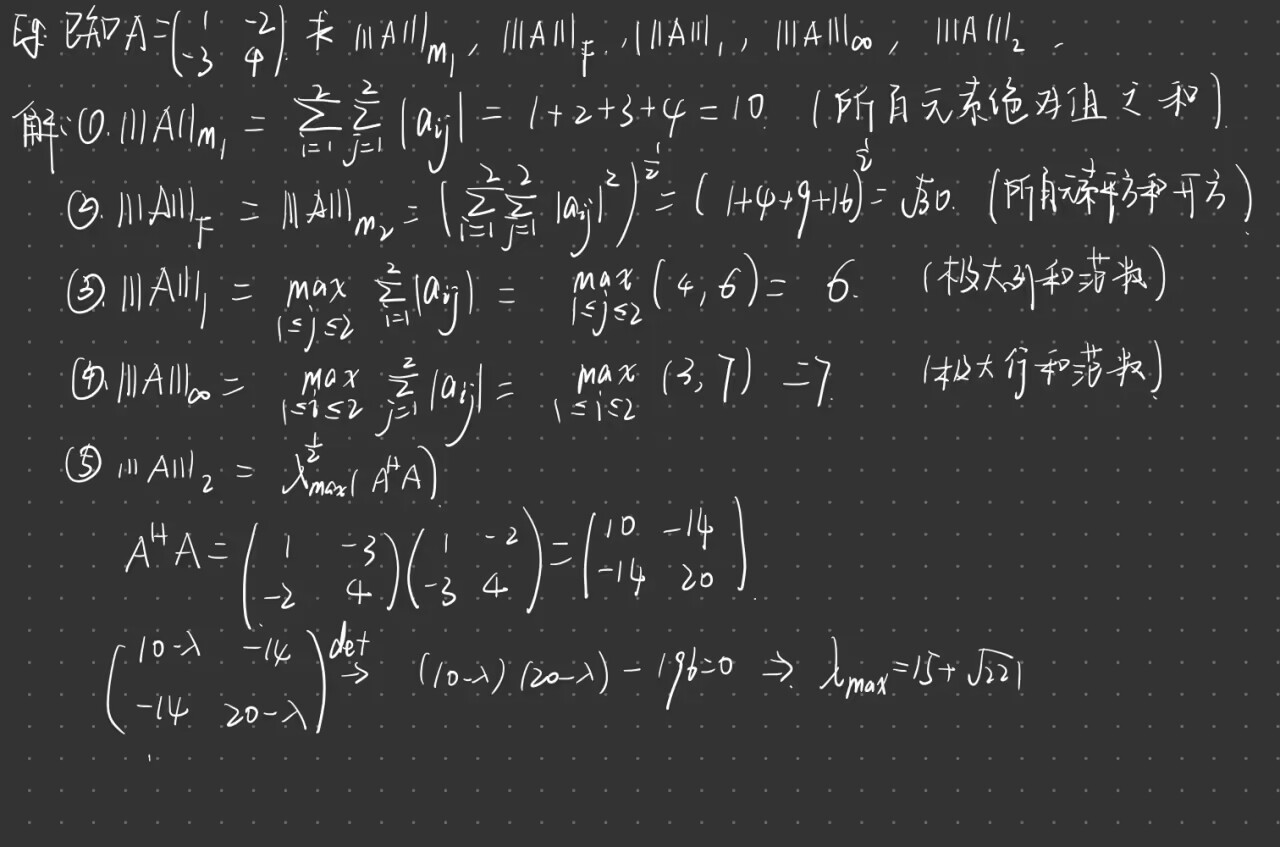
F范数的酉不变性:$A$普通矩阵,$P,Q$都是酉矩阵($P^HP = I$)
$||A|| = ||PA|| = ||AQ|| = ||PAQ||$
矩阵范数等价性:如果能找到$C_1, C_2$
$C_1||A||_s \leq ||A||_t \leq C_2||A||_s$ , 则$||\cdot||_s $与$||\cdot||$等价
比如 $\frac{1}{\sqrt{n}}||A||_F \leq ||A||_2 \leq ||A||_F$
谱半径:
- 定义:$\rho(A) = \underset{1 \leq i \leq n}{\max} | \lambda_i| $ , 其中$\lambda$为$A$的特征值
- 与矩阵范数的关系:$\rho(A) \leq ||A||$ 但是,存在一种矩阵范数使得$||A||_{\epsilon} < \rho(A) + \epsilon$
谱范数的性质:
- $||A||_2 = \underset{||x||_2 = 1, ||y||_2 = 1}{\max} ||y^HAx|| $
- $||A^H||_2 = ||A||_2 = ||A^T||_2$
- $||A^HA|| = ||A||_2^{2}$
- 对正规矩阵A有:$\rho(A) = ||A||_2$
- 对非奇异矩阵A有:$||A||_2 = \rho(A^HA)^{\frac{1}{2}}$
1.1.3 范数的应用
衡量 $A^{-1}$与$(A + \delta A)$的误差:
要求 $||A^{-1} \delta A || < 1$, 则。。。
条件数:$cond(A) = ||A||||A^{-1}||$
病态方程:$Ax=b$如果$A$发生微小变化时,解发生巨大变化
2. 特殊矩阵
2.1 置换矩阵
2.1.1 Hermite矩阵
- 对称矩阵:$A^T = A, A \in R^{n \times n}$
- Hermite矩阵:$A^H = A, A \in C^{n \times n}$
- A为Hermite矩阵,$A+A^H, AA^H, A^HA ,A^{-1}$也是Hermite矩阵
- A,B为Hermite矩阵, $\alpha A + \beta B$也是Hermite矩阵
- Hermite矩阵正定的条件:
- A所有特征值大于0
- 存在一个非奇异R,使得$A = R^HR$
- 对任意非奇异P,有$P^HAP$正定
2.1.2 置换矩阵
- 置换矩阵:方阵,每行每列只有一个1,其余全为0
- 性质:
- $P^T$也是置换矩阵
- $P^T P = PP^T = I$
- $P^T = P^{-1}$
- 移位矩阵:$p_{i, i+1} = 1, p_{n1} = 1$,其余为0, $P_n = (e_n, e_1, ..,e_{n-1})$
2.1.3 广义置换矩阵
定义:每行每列仅有一个非0元素
$G = P D$,$G$为广义置换矩阵,$P$为置换矩阵,$D$为非奇异的对角阵
选择矩阵:对矩阵的某些行或者某些列进行选择
$J_1 = (I_{m-1}, 0_{m-1}), J_1x = (x_1, x_2,..,x_{m-1})^T$, 选择了前m-1行
2.2 正交矩阵与酉矩阵
- 正交矩阵:$Q^TQ = QQ^T = I$
- 酉矩阵:$U^H U = U U^H = I$
- A与B酉相似:$B = U^HAU = U^{-1}AU$
- 性质:
2.3 三角矩阵
- 性质:
- 上三角矩阵乘积为上三角矩阵
- 上三角矩阵行列式是对角线元素乘积
- 上三角矩阵逆也是上三角矩阵
- 正定的Hermite矩阵,能$A = T^H DT$, $T$单位上三角
- 正定矩阵A ,能有$AA = L L^T$
2.4 Hardmard矩阵
2.5 Toplitz矩阵与Hankel矩阵
3. 矩阵变换与分解
3.1 酉变换(正交变换)
3.1.1 酉等价(酉相似)
- 定义:
- 性质:
- 酉等价 —> 相似
- 对酉变换$y = Ux$ ,不改变向量长度
3.1.2 Givens变换(初等旋转变换)
定义
性质
求Givens矩阵
例题

3.1.3 Householder变换(初等反射变换)
定义
性质
求取Householder矩阵
例题
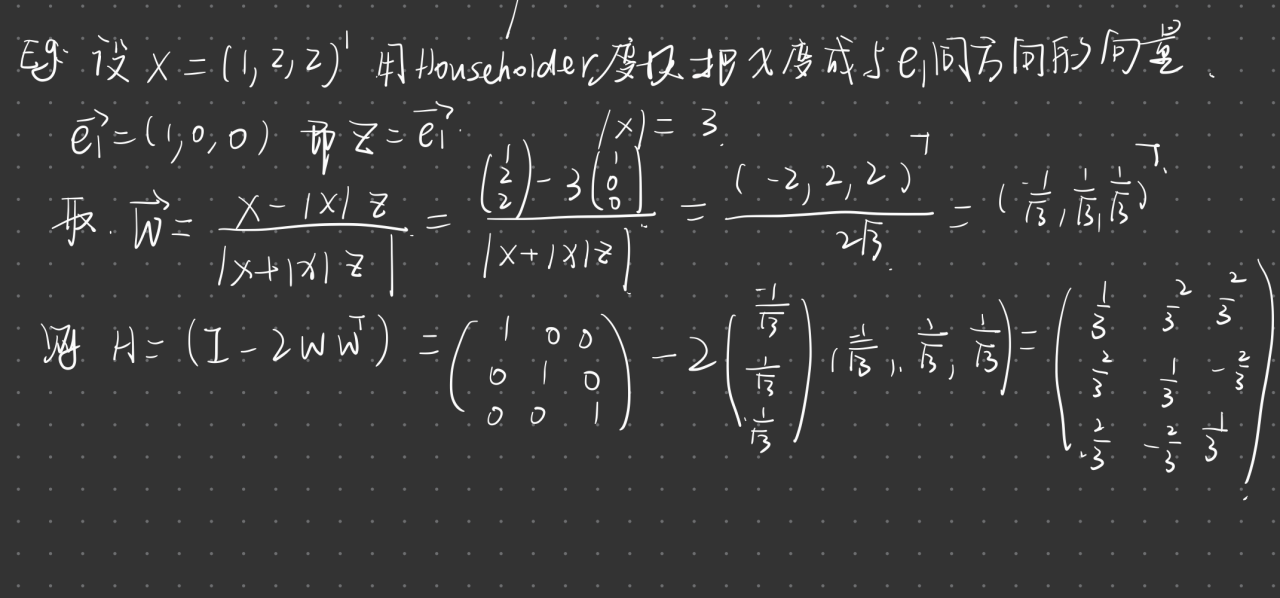
Givens变换 是 两个 Householder变换 的乘积
3.2 QR分解
定义:把矩阵分解成 正交矩阵 和 上三角矩阵 的乘积
使用Givens变换做矩阵的QR分解
使用Householder变换做矩阵QR分解
例题1
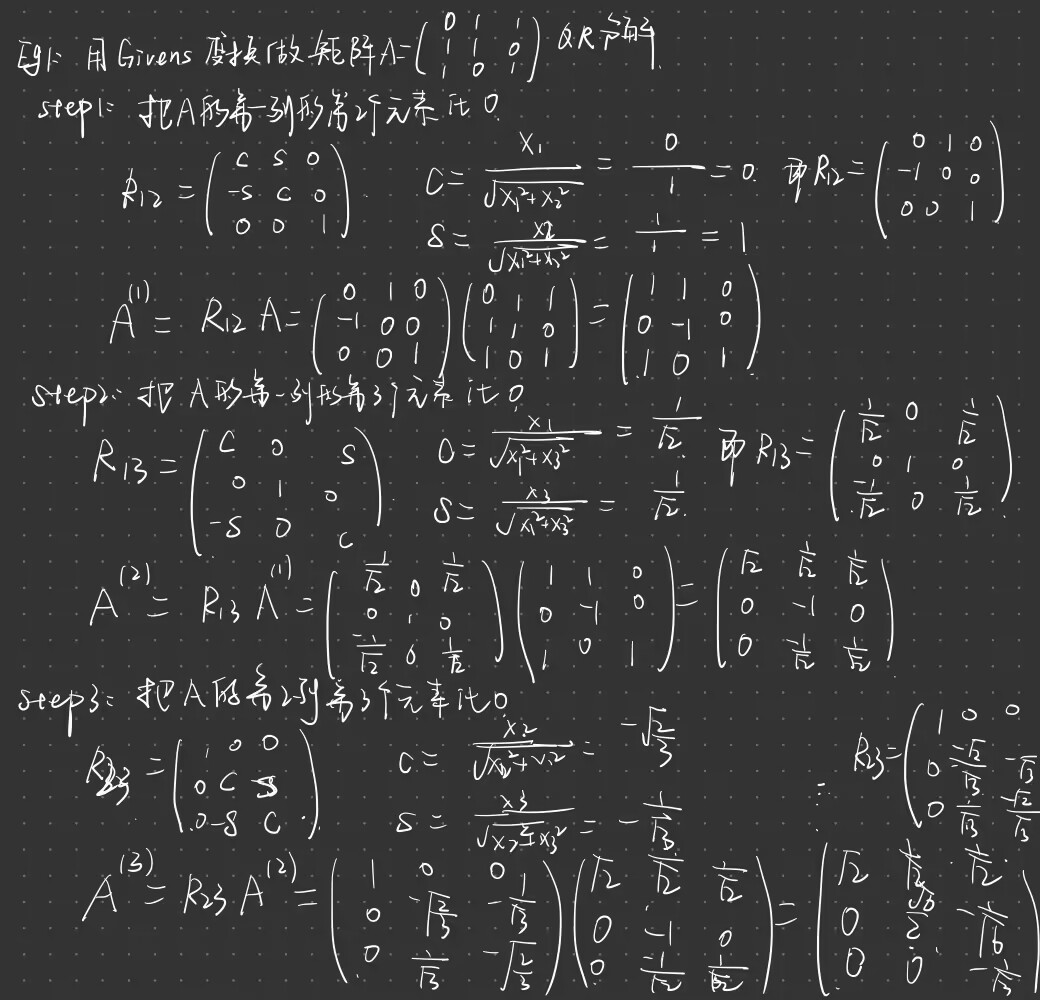
例题2

Hessenberg正交相似:
上H矩阵:对任意的$i\geq j+2$, $h_{ij} = 0$
对任意方阵$A$,存在正交矩阵$P$,使得$P^{-1}AP = H$
3.3 Schur分解
Schur定理: 矩阵A 能 酉相似于 上三角矩阵 即($U^H A U = T$)
正规矩阵:$AA^H = A^HA$
与正规矩阵酉等价的矩阵都是正规矩阵
如:Hermite矩阵 、反Hermit矩阵、 酉矩阵
定理1: A酉相似于对角矩阵 等价于 A是正规矩阵
各类正规矩阵的特征值:
- Hermite矩阵($A^H = A$):实数
- 反Hermite矩阵($A^H =-A$):0或者纯虚数
- 实对称矩阵($A^T = A$):实数
- 反实对称矩阵($A^T =-A$):0或者纯虚数
正规矩阵$A^H$的特征值为$\bar{\lambda}$,特征向量为$x$
正规矩阵的特征向量两两正交
正规矩阵的相似对角化:利用原理$Au_i = \lambda_iu_i$,$U$的每列就是$A$的特征值对应的特征向量
例题:
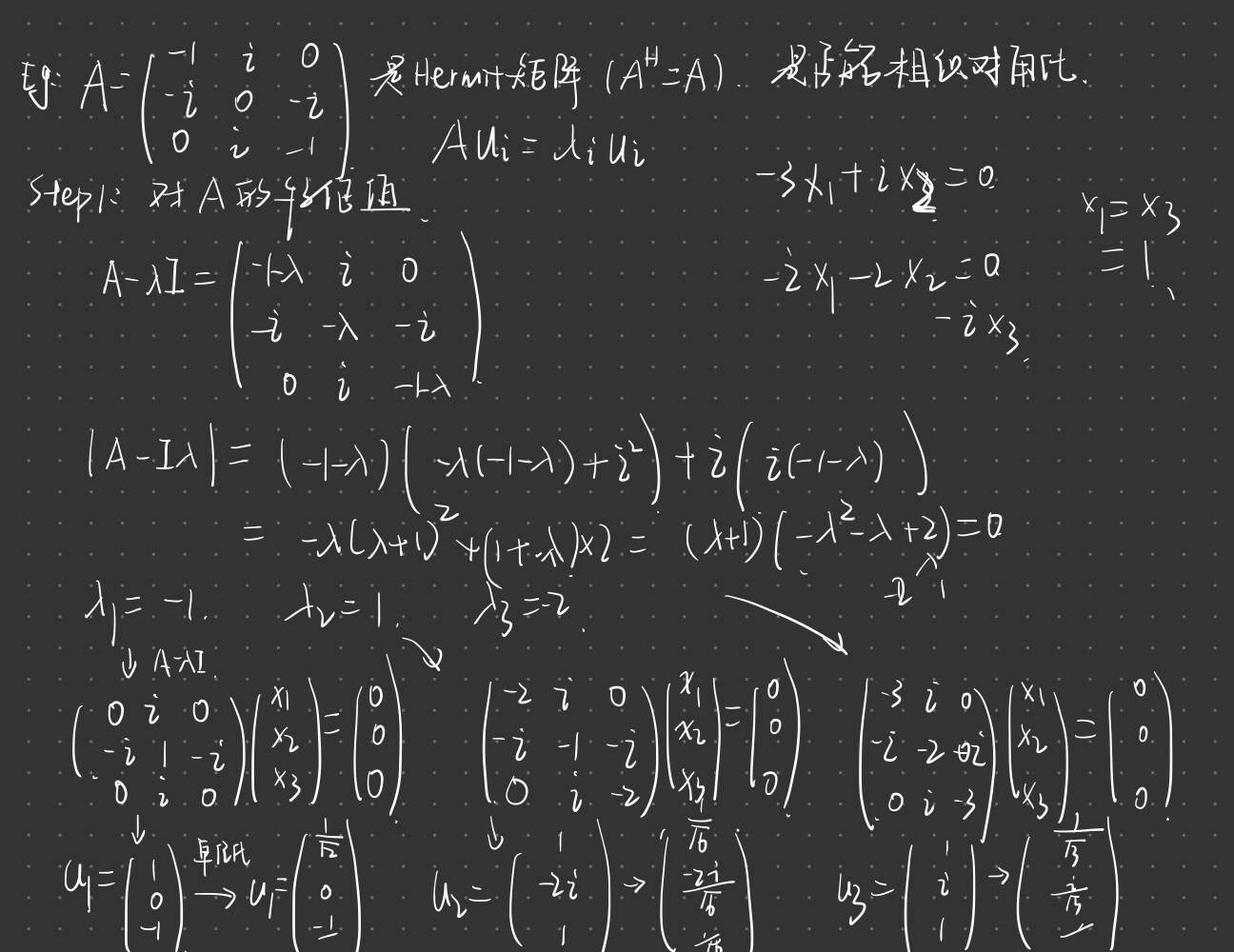
3.4 Jordan标准型与谱分解
3.4.1 预备知识
- 特征值与特征向量
- -A的特征值为$-\lambda$,特征向量为$x$
- 设$B$与$A$相似,有$P^{-1}AP =B$,则B的特征值也是$\lambda$,特征向量为$P^{-1}x$
- AB 与 BA 具有相同的特征值
- 若A能相似对角化 等价于 A与对角阵 相似
3.4.2 Jordan标准型
Jordan标准型定义:对矩阵$A \in C^{n * n}$,存在非奇异的$P$,使得$P^{-1}AP = diag(J_1, J_2,…,J_s)$,$J_i$为Jordan块。
若 $J_i$都是一阶的,则A非亏损,否则 亏损
$\lambda$矩阵与特征矩阵:
$\lambda$矩阵:$A(\lambda)=(a_{ij}(\lambda))$
特征矩阵:$\lambda I - A$
$\lambda$矩阵的秩:$\lambda$矩阵的不为0的子式的最大阶数
$\lambda$矩阵的三种初等变换:
- 任意两行或者两列位置互换
- 某一列或行 乘以 非0常数
- 某一列或行 乘以 $\phi(\lambda)$加到某列或行
$\lambda$矩阵的等价:$A(\lambda)$可以经过一系列初等变换为$B(\lambda)$
$\lambda$矩阵的标准形:把$A(\lambda)$通过若干初等变换成$diag(d_1(\lambda), d_2(\lambda), …,d_r(\lambda),0,,,0 )$,且$d_i(\lambda)| d_i+1(\lambda)$,$d_i(\lambda)$叫做不变因子, 如$d_1(\lambda)= 1, d_2(\lambda)= \lambda,d_3(\lambda)= \lambda^2 + \lambda$
例题
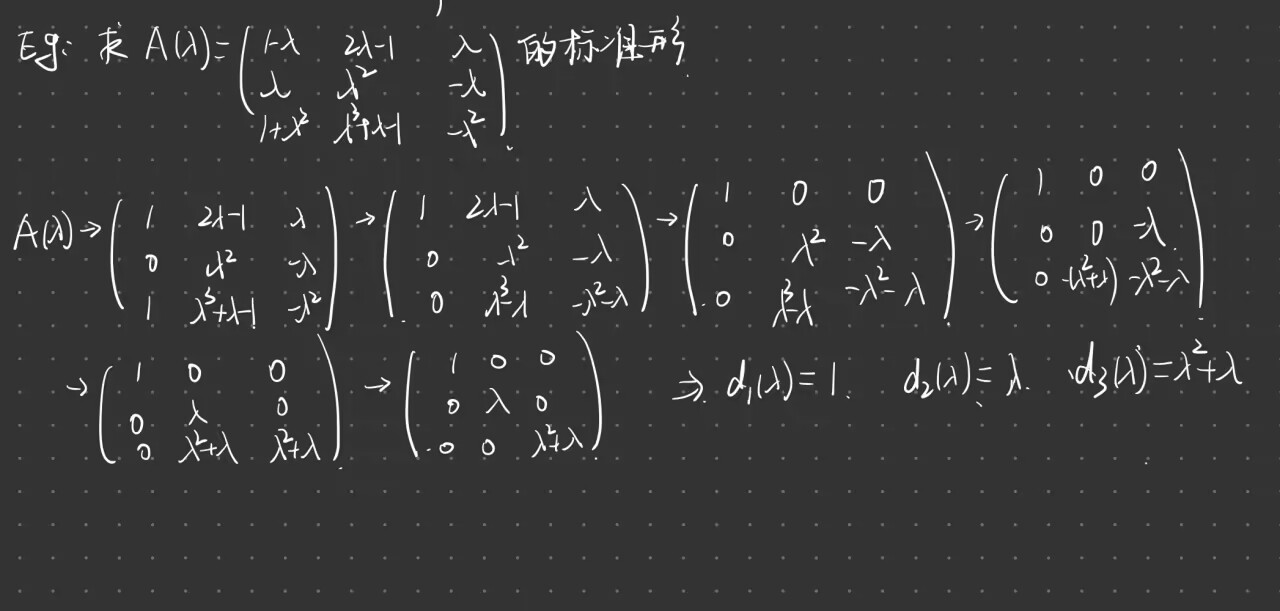
$\lambda$矩阵的k阶行列式因子:$\lambda$矩阵的所有$k$阶子式的行列式的首一的最大公因式
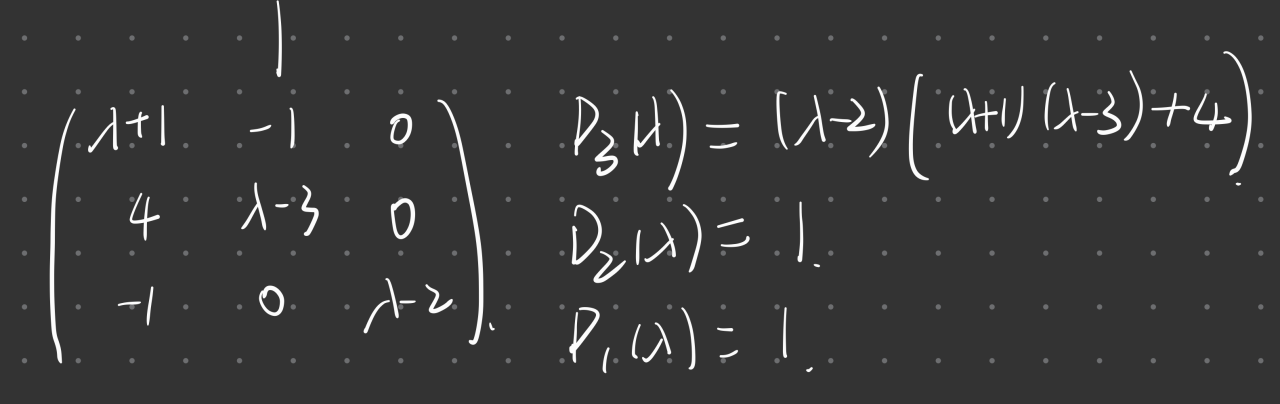
且 $D_k(\lambda) = d_1(\lambda)…d_k(\lambda)$, $d_k(\lambda) = \frac{D_k(\lambda)}{D_{k-1}(\lambda)}$
$A(\lambda)$等价于$B(\lambda)$ 当且仅当 两者有相同的 行列式因子 和 不变因子
$\lambda$矩阵的初等因子:把次数大于0的不变因子 分解成 互不相同的首1的不可约因式的乘积
例题:

Jordan标准型的全部初等因子 等于 每个Jordan块的初等因子 $(\lambda - \lambda_1)^{k_1}, (\lambda - \lambda_2)^{k_2}, ,,,(\lambda - \lambda_s)^{k_s}$
已知初等因子 反推其Jordan块:
- 求$\lambda I - A$的全部初等因子 $(\lambda - \lambda_1)^{k_1}, (\lambda - \lambda_2)^{k_2}, ,,,(\lambda - \lambda_s)^{k_s}$
- 求每一个Jordan块
- 组合全部的Jordan块得到Jordan标准型
例题

谱分解:一个n阶方阵可对角化 等价于 A有n个线性无关特征向量
$A = \sum_{i=1}^n \lambda_i x_i y_i^T$ ($x_i$为特征值$\lambda_i$对应右特征向量, $y_i$是左特征向量 $A^T y_i = \lambda_i y_i$)
3.5 Gauss变换与三角分解
3.5.1 Gauss变换
- Gauss向量与Gauss矩阵:
- Gauss向量:$g^{(k)} = (0,0,…0,g_{(k+1)k},..,g_{nk})^T$
- Gauss矩阵:$G_k = I - g^{(k)}e_k^{T}$ (初等下三角矩阵)
- Gauss矩阵逆矩阵:$G_k^{-1} = I + g^{(k)}e_k^{T}$
- 性质:
- $G_k x = (x_1, x_2,…,x_k,0,…,0)$
3.5.2 Gauss消元与三角分解
Gauss消元:
$Ax = b$
- step1:$L_1 = I - l^{(1)}e_1^{T} , (l_{i1} = \frac{a_{i1}^{(1)}}{a_{11}^{(1)}})$, $A^{(2)} = L_1 A^{(1)}$, $b^{(2)} = L_1 b^{(1)}$ 此时$A^{(2)}$的第一列的对角线下方全为0
- step2:$L_2 = I - l^{(2)}e_2^{T} , (l_{i2} = \frac{a_{i2}^{(2)}}{a_{22}^{(2)}})$, $A^{(3)} = L_2 A^{(2)}$, $b^{(3)} = L_2 b^{(2)}$ 此时$A^{(3)}$的第一,二列的对角线下方全为0
- 一直做n-1次
三角分解:n阶方阵分解成一个下三角矩阵L和一个上三角矩阵U的乘积 $A = LU$
- 分类:
- Doolittle分解:$A = LU$ ($L$是单位下三角,U上三角)
- Crout分解:$A = LU$ ($L$是下三角,U单位上三角)
- LU分解不唯一 $A = LU = LDD^{-1}U = L^{‘}U^{‘}$, $D$为对角矩阵
- 定理1:对非奇异的n阶方阵,其各阶顺序主子式不为0,则A可以做三角分解,且分解唯一 , $A = LDU$, $d_k = \frac{\triangle_k}{\triangle_{k-1}}$
- 分类:
例题:
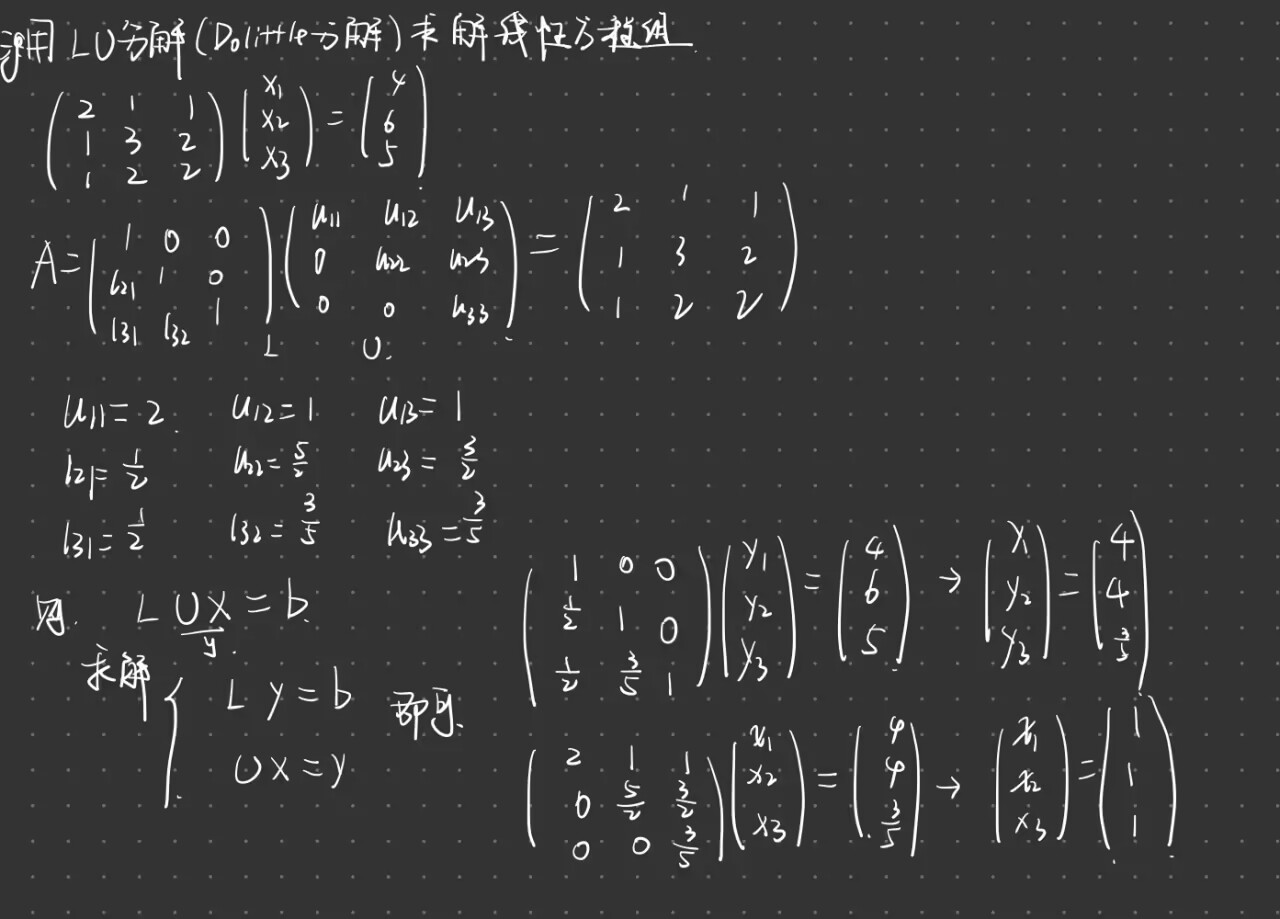
Cholesky(平方根分解)
定理:对对称正定的$A$,存在唯一的对角线为正的下三角矩阵$L$,使得$A = L L ^T$
例题:
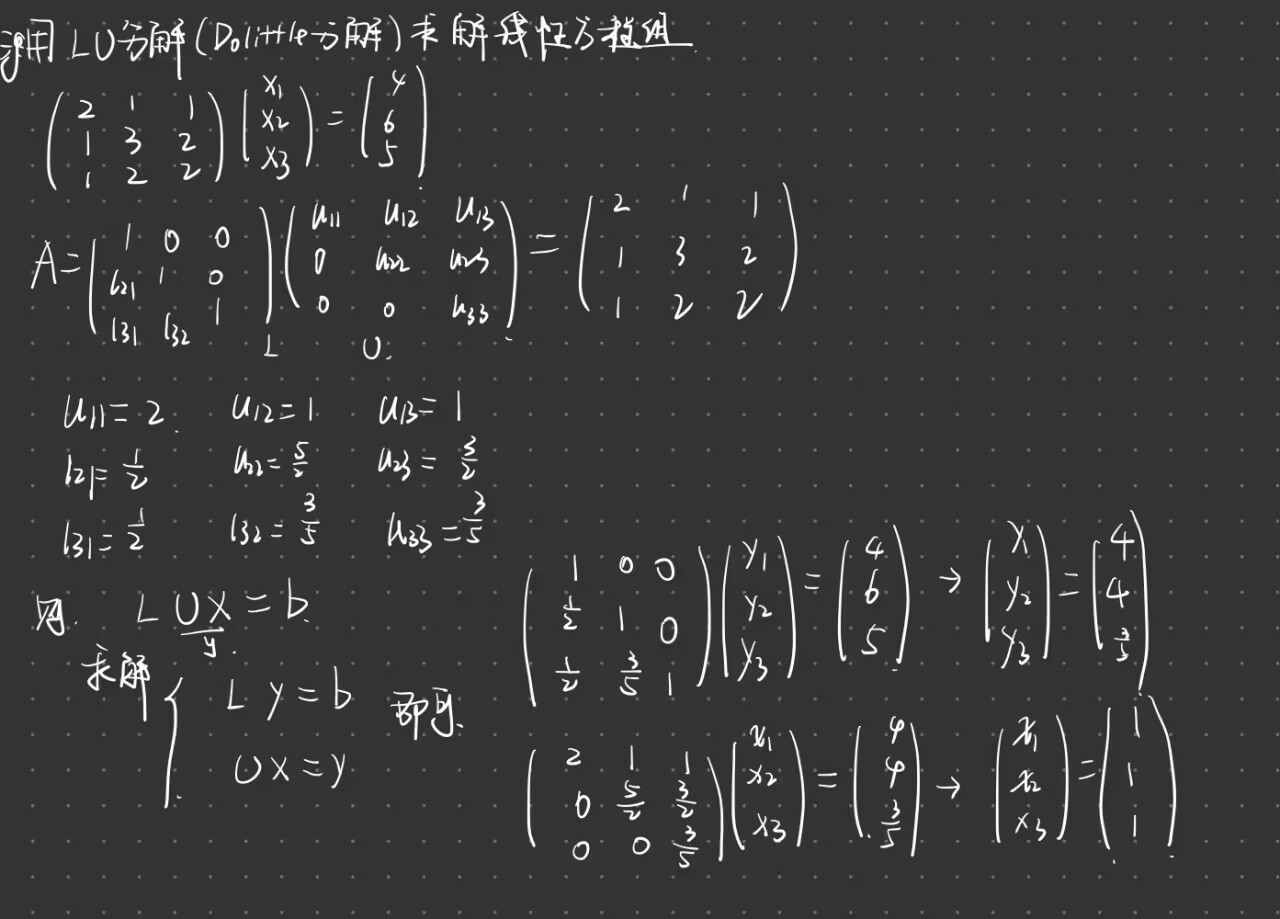
3.6 最大秩分解
最大秩矩阵:$A = (a_{ij})_{m \cdot n}$, 若$m \leq n, Rank(A) = m$,被称作行最大秩矩阵; 若$m \geq n, Rank(A) = n$,被称作列最大秩矩阵
满秩分解:$A = (a_{ij})_{m \cdot n}, rank(A) = r$,一定存在$B \in C^{m \cdot r}_r, C \in C^{r \cdot n}_r$,使得$A = BC$
举例:
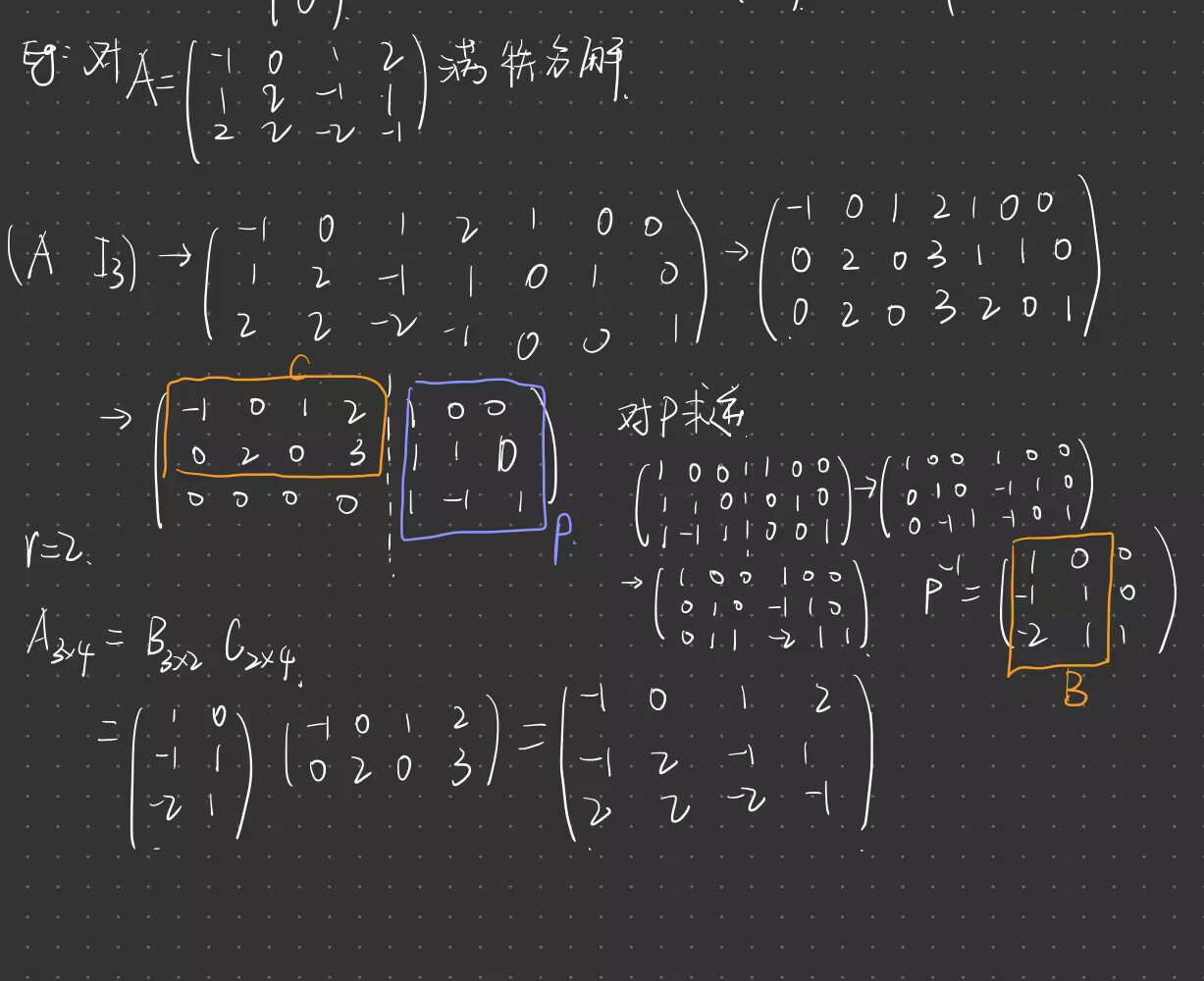
3.7 奇异值分解
- 定义:对矩阵$A$,存在正交矩阵或酉矩阵$U,V$,使得$$A = U \begin{bmatrix} \Sigma_r & 0 \ 0 & 0 \end{bmatrix} V^{T}$$, 其中$\Sigma_r = diag(\sigma_1,..,\sigma_r)$
- 例题:
