diffusion模型介绍

Diffusion模型

1 介绍

扩散模型本质是学习真实的数据分布，从而从中抽样，生成新样本。

diffusion过程：不断给真实图片加噪声，直至变成纯噪声。如何，训练一个解码器去噪，逐步进行，直至回复成原本的真实样本。

2 生成模型的目标

学习到的数据分布要尽可能符合原始训练数据分布。

$P_{\theta}(x)$模型所产生的图片的改了分布， $\theta$表示模型的参数
$P_{data}(x)$训练数据的概率分布，也就是真实图片的分布，$data$表示真十四数据，与模型无关。

为了衡量这两个分布之间的距离，通常使用KL散度，则目标函数表示如下：

$$ \begin{align}
\arg\min_{\theta} KL(P_{data}||P_{\theta}) &= \arg\min_{\theta} \int_x P_{data}(x) \log\frac{p_{data}(x)}{p_{\theta}(x)} \
&= \arg\min_{\theta} \left( \int_x P_{data}(x) \log P_{data}(x) - \int_x P_{data}(x) \log p_{\theta}(x) \right) \ &= \arg\max_{\theta} \left( \int_x P_{data}(x) \log p_{\theta}(x) - \int_x P_{data}(x) \log P_{data}(x) \right) (第二项为常数) \ &= \arg\max_{\theta} \int_x P_{data}(x) \log p_{\theta}(x) \ &= \arg\max_{\theta} E_{x~P_{data(x)}} \log p_{\theta}(x) \ & \approx \arg\max_{\theta} \sum_{i=1}^{m} \log p_{\theta}(x_i) (近似为从真实世界抽样m张图片) \ &= \arg\max_{\theta} \log \prod_{i=1}^{m} p_{\theta}(x_i) \ &= \arg\max_{\theta} \prod_{i=1}^{m} p_{\theta}(x_i)
\end{align} $$

从上述推导过程，我们发现，优化目标变成了使得模型产生真实图片的概率最大

3 前向噪声扩散

向原始图片逐步添加高斯噪声，直至最后的图像趋于高斯分布。

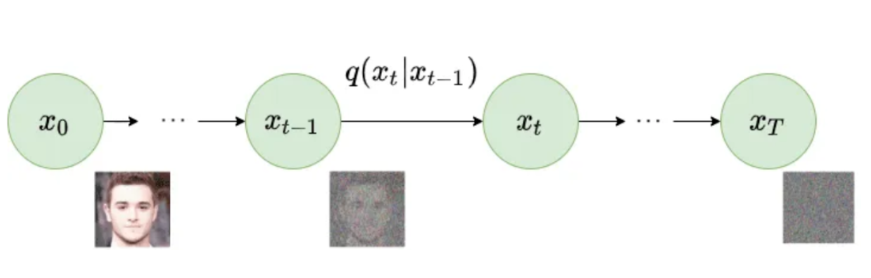
下面推导如何从初始图像得到第$t$时刻的图像：

$ x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1- \alpha_t} \epsilon_t, \epsilon_t \in N(0,1), i.i.d$

$$ \begin{align}
q(x_t| {x_{t-1}}) &= N(x_t; \sqrt{\alpha_t} x_{t-1}, (1-\alpha_t)I) \ &= \sqrt{\alpha_t} x_{t-1} + \sqrt{1- \alpha_t} \epsilon_t \ &= \sqrt{\alpha_t} ( \sqrt{\alpha_{t-1 } } x_{t-2} + \sqrt{1- \alpha_{t-1} } \epsilon_{t-1} ) + \sqrt{1- \alpha_t} \epsilon_t \ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}} \epsilon_{t-1} + \sqrt{1- \alpha_t} \epsilon_t \ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{1- \alpha_t \alpha_{t-1} }\epsilon (两个相互独立的正态分布相加，又均值为0，只用考虑方差) \ &= \sqrt{\alpha_t \alpha_{t-1} \alpha_{t-2} … \alpha_{1}}x_0 + \sqrt{1 - \alpha_t \alpha_{t-1} \alpha_{t-2} … \alpha_{1}} \epsilon \ &= \sqrt{\overline{\alpha_t}} x_0 + \sqrt{1 - \overline{\alpha_t}} \epsilon
\end{align} $$

4 反向扩散过程

由 $x_{t}$到$x_{t-1}$

$P(x_{t-1} | x_t) = N(x_{t-1}; u_{\theta}(x_t, t), \sum_{\theta}(x_t, t) )$

在第2节中，我们提到了生成模型的目标，即$\arg\max_{\theta} \prod_{i=1}^{m} p_{\theta}(x_i)$

这里的$x$是指前扩散的初始图像，以后都记为$x_0$，在反向扩撒的过程中，它依赖于$x_0$之前的所有步长，从$x_T$开始往后。。。

$\log P(x_0) = \log \frac{P(x_0, x_1, x_2,…,x_T)}{ P(x_1,x_2,…,x_T | x_0)} (马尔科夫链的公式)$

上式关于$q_{(x{1:T} |x_0)}$积分

等式左边：$\int \log P(x_0) q_{(x{1:T} |x_0)} dx_{1:T} = \log P(x_0)$

等式右边：$\int \log \frac{P(x_0 :T)}{P(x_{1:T} |x_0) } q(x_{1:T} | x_0) dx_{1:T}$

故：$\log P(x_0) = \int \log \frac{P(x_0 :T)}{P(x_{1:T} |x_0) } q(x_{1:T} | x_0) dx_{1:T}$

右侧的式子经过变形可以化成以下形式：

$\log P(x_0) = \int \log \frac{P(x_{0:T})}{q(x_{1:T} | x_0)} q(x_{1:T } |x_0) dx_{1:T} + KL(q(x_{1:T} | x_0) || P(x_{1:T}|x_0))$

上述等式右边第二项有一个KL散度，但是我们并不知道$P(x_{1:T}|x_0)$，如果我们能求出$q(x_{1:T} | x_0)$，又KL散度是一个大于等于0的数，当两个概率分布相等时，KL=0，只需让右式第二项最小即可。

即最小化$ KL(q(x_{1:T} | x_0) || P(x_{1:T}|x_0))$

对于确定的训练数据$x_0$与其似然参数，$\log P(x_0)$是唯一确定的。如果最小化第二项，则最大化了第一项。

由于第二项散度恒大于等于0，所以对于第一项①，$\log P(x_0) \geq ①$， ①也被称作变分下界。

$$ \begin{align}
\log P(x_0) & \geq \int \log \frac{P(x_{0:T})}{q(x_{1:T} | x_0)} q(x_{1:T } |x_0) dx_{1:T} \ &= \mathbf{E}q[ \log \frac{P(x{0:T})}{q(x_{1:T} | x_0)}] \ &= \mathbf{E}q [\log \frac{P(x_T) P(x{0:T-1} | x_T)}{q(x_{1:T} | x_0)} ] \ &= \mathbf{E}q [\log P(x_T) + \log \frac{P(x{0:T-1} | x_T)}{q(x_{1:T} | x_0)} ] \ &= \mathbf{E}q [\log P(x_T) + \log \frac{\prod{t=1}^T P(x_{t-1} | x_t)}{\prod_{t=1}^T q(x_t | x_{t-1})} ] \ &= \mathbf{E}q [\log P(x_T) + \sum{t=1}^T \log \frac{ P(x_{t-1} | x_t)}{ q(x_t | x_{t-1})} ] \ &= \mathbf{E}q [\log P(x_T) + \sum{t=2}^T \log \frac{ P(x_{t-1} | x_t)}{ q(x_t | x_{t-1})} + \log \frac{P(x_0 | x_1)}{q(x_1 |x_0)} ]
\end{align} $$

再经过一大段推导。。。可以得到最终式子：

$\log P(x_0) \geq \mathbf{E}{q{(x_1|x_0)}}[\log P(x_0 | x_1) ] - \sum_{t=2}^T \mathbf{E}{q(x_t| x_0)} [kL(q(x{t-1}|x_t,x_0) || P(x_{t-1} | x_t))] - KL(q(x_T|x_0) || P(x_T))$

上式就是我们的优化目标！

上式的第三项可以直接求取，没有需要学习的参数

第一项式重构损失，第二项是KL散度，$P(x_{t-1}|x_t)$需要使用神经网络来逼近

对$q(x_{t-1 } | x_t,x_0) $有：

$$ \begin{align}
q(x_{t-1 } | x_t,x_0) & = \frac{q(x_{t-1},x_t | x_0)}{q(x_t |x_0)} \ &= \frac{q(x_t| x_{t-1},x_0)q(x_{t-1} | x_0)}{q(x_t |x_0)} \ &= \frac{N(\sqrt{\alpha_t} x_{t-1}, (1- \alpha_t)I) N(\sqrt{\overline{\alpha}{t-1}} x_0, (1- \overline{\alpha}{t-1})I)}{N(\sqrt{\overline{\alpha_t}} x_0, (1- \overline{\alpha_t})I)}
\end{align} $$

带入正态分布公式展开，可以得到：

$$q(x_{t-1 } | x_t,x_0) \textasciitilde N(x_{t-1} | \frac{\sqrt{\alpha_t}(1-\overline{\alpha}{t-1})x_t}{1- \overline{\alpha_t} } + \frac{\sqrt{\overline{\alpha}{t-1}}\beta_t x_0}{ 1- \overline{\alpha_t}}, \frac{1- \overline{\alpha}_{t-1}}{1- \overline{\alpha}_t}\beta_t I)$$

对上式，$x_0$未知，尝试使用一个新的分布$q(x_{t-1}|x_t)$来替代

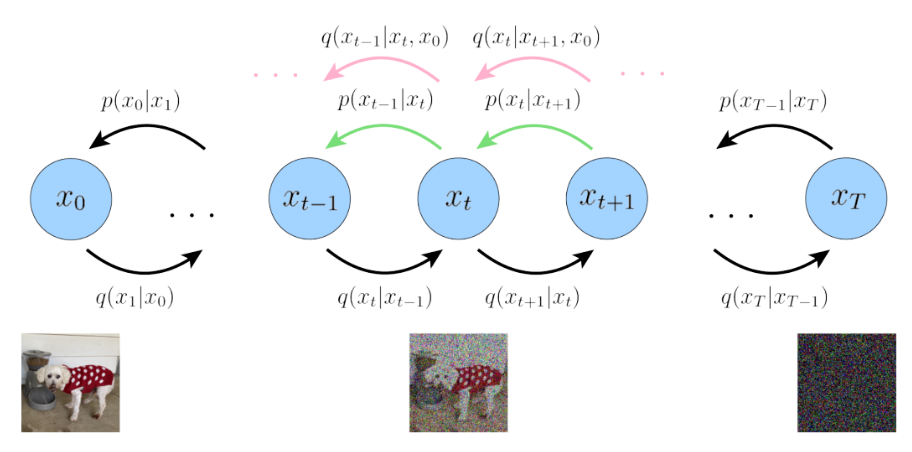
这个新的分布（绿色箭头），使其方差与$q(x_{t-1} | x_t, x_0)$一致，而均值把 $x_0$替换成$\hat{x}_{\theta}(x_t, t)$，即$x_0$由$x_t$和$t$基于一个深度模型预测。

接下来就是缩小$p$和$q$之间的差距，如果直接让模型从$x_t$去预测$x_0$，难度过大，在前面的前向过程中，$x_t = \sqrt{\bar{\alpha_t}}x_0 + \sqrt{(1- \bar{\alpha}_t)}\epsilon$，变成$x_0 = \frac{x_t - \sqrt{1 - \bar{\alpha}_t}\epsilon}{\sqrt{\bar{\alpha}t}}$，带入原来的$q(x{t-1}| x_t, x_0)$的均值里面：$u = \frac{1}{\sqrt(\alpha_t)}x_t - \frac{1- \alpha_t}{\sqrt{1- \bar{\alpha}_t}\sqrt{\alpha_t}}\epsilon$

则，构造的分布$p(x_{t-1}|x_t)$的均值$u = \frac{1}{\sqrt(\alpha_t)}x_t - \frac{1- \alpha_t}{\sqrt{1- \bar{\alpha}t}\sqrt{\alpha_t}}\hat{\epsilon{\theta}}$

这样，把由$x_t$,$t$去预测$x_0$ 变成了由$x_t$,$t$去预测$\epsilon_t$。

Step5就是训练一个模型: $x_0$经过$t$时间步加噪声后的$x_t$ 和时间步$t$ 预测出加的噪声$\epsilon$，深度学习模型是类似 UNet 的结构

5 推理过程

模型训练好之后，在真实的推理阶段就必须从时间步 T 开始往前逐步生成图片，算法描述如下：

先生成一个服从高斯分布的noise: $x_T$

从最后一个时间步开始：由上一步图像$x_t$输入模型去预测噪声$\epsilon_t$，再由冲参数化技巧，计算$x_{t-1}$，一直到时间步1为止，从而生成$x_0$。

6 实现

6.1 Algorithm1: Training

$x_0 $ ——> $x_t$

从数据中抽样本$x_0$
从$1$~$T$中随机抽取一个时间$t$，对该时间步做embedding
$x_0$ + t_embedding ——>(GaussionDiffusion) ——>$x_t$
$x_t$ + t_embedding ——> (Unet) ——> predicted noise
计算 predicted noise 和 GuassionDiffusion采样的noise的loss
重复上述步骤，直至Unet网络训练完成

前向扩散：

""""
    前向扩散：x_0 + t ——> x_t   (x_t =   sqrt(bar{alpha_t})x_0 + sqrt(1 - bar{alpha_t}) epsilon )
"""
def q_x(x_0, t):
    noise = torch.rand_like(x_0)
    alphas_bar_t = alphas_bar_sqrt[t]
    alphas_one_minus_bar_sqrt = one_minus_alphas_bars_sqrt[t]
    x_t = alphas_bar_t * x_0 + alphas_one_minus_bar_sqrt * noise

预测噪声：

"""
    预测噪声的Unet模型（MLP模拟的UNET）
"""
class MLPDiffusion(nn.Module):
    def __init__(self, n_steps, num_units=128):
        super(MLPDiffusion, self).__init__()

        self.linears = nn.ModuleList(
            [
                nn.Linear(2 , num_units),
                nn.ReLU(),
                nn.Linear(num_units, num_units),
                nn.ReLU(),
                nn.Linear(num_units, num_units),
                nn.ReLU(),
                nn.Linear(num_units,2),
                
            ]
        )

        self.step_embeddings = nn.ModuleList(
            [
                nn.Embedding(n_steps, num_units),
                nn.Embedding(n_steps, num_units),
                nn.Embedding(n_steps, num_units),
            ]
        )
        
        
    def forward(self, x ,t):
        for idx, embedding_layer in enumerate(self.step_embeddings):
            t_embedding = embedding_layer(t)
            x = self.linears[2 * idx](x)
            x += t_embedding
            x = self.linears[2 * idx +1 ](x)
        x = self.linears[-1](x)

        return x

6.2 Algorithm2: Sampling

$x_t$ ——> $x_{t-1}$

从N(0,1)中采样$x_T$
对 $T, T-1, T-2,…,2,1$ 依次重复一下步骤：
$x_t$ + t_embedding ——> (Unet) ——> predicted noise

$x_t$ - predicted_noise ——> $x_{t-1}$
循环结束得到$x_0$

单步逆扩散过程：

def p_sample(model, x, t, betas, one_minus_alphas_bar_sqrt):
    """
        由 x_t 去噪得到 x_{t-1}
    """
    t = torch.tensor([t])
    coeff = betas[t] / one_minus_alphas_bar_sqrt[t]

    eps_theta = model(x ,t)
    mean = (1 / (1 - betas[t]).sqrt()) * (x  - (coeff * eps_theta))
    # 采样得到 x_{t-1}
    z = torch.rand_like(x)
    sigma_t = betas[t].sqrt()
    sample = mean + sigma_t * z
    return sample

循环逆扩散过程：

def p_sample_loop(model, noise_x_t, n_steps, betas, one_minus_alphas_bar_sqrt):
    """
        x[T] ——> x[T-1] ——> x[T-2] ——> ... ——> x[0]
    """
    cur_x = noise_x_t
    x_seq = [noise_x_t]
    for i in reversed(range(n_steps)):
        cur_x = p_sample(model, cur_x, i, betas, one_minus_alphas_bar_sqrt)
        x_seq.append(cur_x)
    return x_seq, cur_x

从N(0,1)中采样$x_T$
对 $T, T-1, T-2,…,2,1$ 依次重复一下步骤：
$x_t$ + t_embedding ——> (Unet) ——> predicted noise

$x_t$ - predicted_noise ——> $x_{t-1}$
循环结束得到$x_0$

diffusion模型介绍

https://wendyflv.github.io/2024/09/07/diffusion模型介绍/

作者

Wendyflv

发布于

2024年9月7日

许可协议

CLIP模型原理及实现上一篇

文生图的各种模型下一篇