基于SMPL的单目3D人体姿态估计
基于SMPL的单目3D人体姿态估计——驱动virtual Avatar
输入一段视频——>
对每一帧—SMPLer—>进行3D形状和姿态估计($\theta$,$cam$,$\beta$)
1. SMPLer
前向传播:
Step1:提取图片全局特征 img——>(HRNet)——>global_feat
Step2:计算初步的SMPL参数 global_feat——>(FC+dropout)——>theta, beta, cam ——>SMPL模型——>smpl_joints, 2Djoints
Step3:融合初始查询向量 beta,theta,cam + global_feat ——>query
Step4:Transfomer层
- query + feat_list——>(全局多尺度单元)——> global_query
- query[:,:-2] + local_feat_list + 对应的local_spat_list ——> (局部多尺度单元)——> local_query
- 0.5(global_query[:,:-2] + local_query) ——> global_query——> (self trans)——> query_embed
1.1 New Contributions
解耦的注意力机制:target-feature target-target
相较于全局注意力,把原二次方的计算降低到线性
多尺度注意力模块 和 关节感知注意力模块
基于参数化的SMPL模型的目标表示,只需要学习人体形状和三维身体旋转参数,使得学习的目标嵌入减少。
1.2 Related Work
GraphCMR(GNNS)、
SPIN、RSC-Net(CNNS)、
METRO、Mesh Graphormer(ViT)
2 Attention
$h(Q,K,V) = softmax(\frac{(QW_q)(KW_k)^T}{\sqrt d})(VW_v)$
Q:Query查询矩阵 $\in R^{l_Q \times d}$
K:Key键 $\in R^{l_K \times d}$
V:Value值 $\in R^{l_K \times d}$
$h(Q,K,V) \in R^{l_Q \times d}$ 又可看作一个新的Q
When query, key and value are the same, Eq. 1 is called self-attention which we denote as $h_{self}(Q) = h(Q, Q, Q)$
When only key and value are the same while query is different, the operation becomes cross-attention, denoted as $h_{cross}(Q, K) = h(Q, K, K)$.
2.1 全局Attention
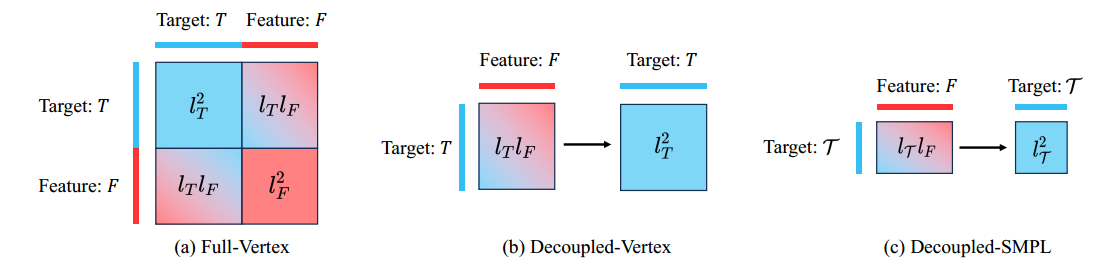
$h_{self}(T||F)$ 即 Q 是将 目标特征 和 目标嵌入 进行concatenation
$T||F \in R^{(l_T+l_F, d)}$ 进行self-attention时会造成二次计算 $O((l_F +l_T)^2)$
2.2 解耦Attention
建模特征-特征依赖关系在3D姿态估计中不太重要,因此全局Attention可以改进为一下公式:
$h_{self}(h_{cross}(T,F))$ 复杂度 $O(l_T l_F + l_T^2)$ 避免了$l_F$的二次计算,而是线性的
3. 目标特征的表示
虽然注意解耦策略有效地减轻了计算负担,但较大的lT仍可能阻碍高分辨率特征的利用。
以往的工作都是回归SMPL的顶点坐标$Y \in R^{N \times 3}$作为目标,但是这里的$N=6890$会导致注意力操作的计算量和内存消耗也很大
为此设计一个基于参数化人体模型SMPL的更紧凑的目标表示是有必要的。
SMPL是一种灵活且具有表现力的人体模型,已广泛应用于三维人体形状和姿态建模。它由一组姿态参数$θ∈ R^{ H×3}$和一个紧致形状向量$β∈R^{1×10}$来参数化。
通过$\theta, \beta$ 可以得到3D的身体mesh:$Y \in R^{N \times 3} = f_{SMPL }(\theta, \beta)$
对顶点做线性映射可得到3D关节坐标:$J \in R^{H \times 3} = M Y$
如果有相机参数$C \in R^3$,可通过弱透视投影计算得到2D关节坐标:$\mathcal{J}= \Pi_C (J) $
故对目标${\theta_i }_{i=1}^H, \beta, C$可表示为$\mathcal{T} \in \mathbb{R}^{(H+2) \times d}$
4. 多尺度注意力设计
4.1 结合多尺度特征
$h_{ms}(\mathcal{T, \mathcal{F}} )= \frac{1}{S} \sum_{i=1}^{S}h_{cross}(\mathcal{T}, F_i)$
为每个尺度使用不同的投影权重,输出是所有尺度的平均值
4.2 多尺度特征位置编码
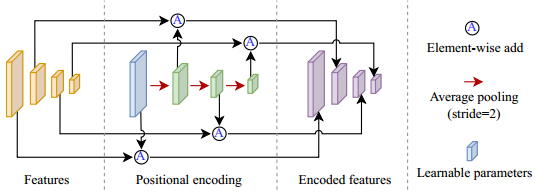
我们对目标和特征使用可学习的位置编码,通常采用x + φ的形式,其中φ是一组可学习的参数,表示标记x的位置信息。
只学习最高尺度的位置嵌入,即ϕ1,而其他尺度的嵌入是通过聚集ϕ1来产生的:

递推可得:$\phi_i = f_{pool}^2(\phi _{i-1})$
5. 关节感知注意力
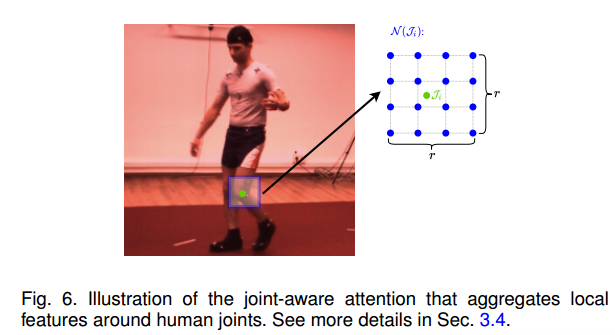
人体关节周围的局部关节状态强烈暗示了邻近身体部位之间的相对旋转。$F_1^{\mathcal{N}(\mathcal{J}_i)}$局部特征是从最高分辨率的图像特征(F1)中采样得到的,覆盖了以关节为中心的r×r大小的区域。
由此,对$\mathcal{T}_i$关节,有如下cross-attention:
$h_{ja}(\mathcal{T}i, \mathcal{F}) = f{soft}(\frac{(QW_q)(KW_k)^T}{\sqrt{d}} + \eta) (F_1^{\mathcal{J}_i}W_v)$
在softmax函数中加入了一个相对位置编码$η∈ \mathbb{R}^{1 \times r^2} $, 它是从一个可学习的张量中根据$\mathcal{J}_i$与$N (\mathcal{J}_i)$中像素之间的距离进行双线性采样。
与多尺度注意力结合,取平均值即可。
$$h_{co}(\mathcal{T}i, \mathcal{F}) = \begin{cases} \frac{1}{2}(h{ja}(\mathcal{T}i, \mathcal{F}) + h{ms}(\mathcal{T, \mathcal{F}} ) ), i \leq H \ h_{ms}(\mathcal{T, \mathcal{F}} ), i >H \end{cases}$$
注意力模块的最终公式:
$h_{final}(\mathcal{T}, \mathcal{F}) = h_{self}(h_{co}(\mathcal{T}, \mathcal{F}))$
6. 整体结构
当前设计的一个重要问题是关节感知注意力依赖于二维关节$J$,这应该是我们算法的一个输出。
换句话说,我们需要$J$来重构三维人,同时需要三维人来回归$J$。为了避免这个问题,SMPLer提出了一个层次结构来迭代地改进二维联合估计和三维重建结果。见下图。
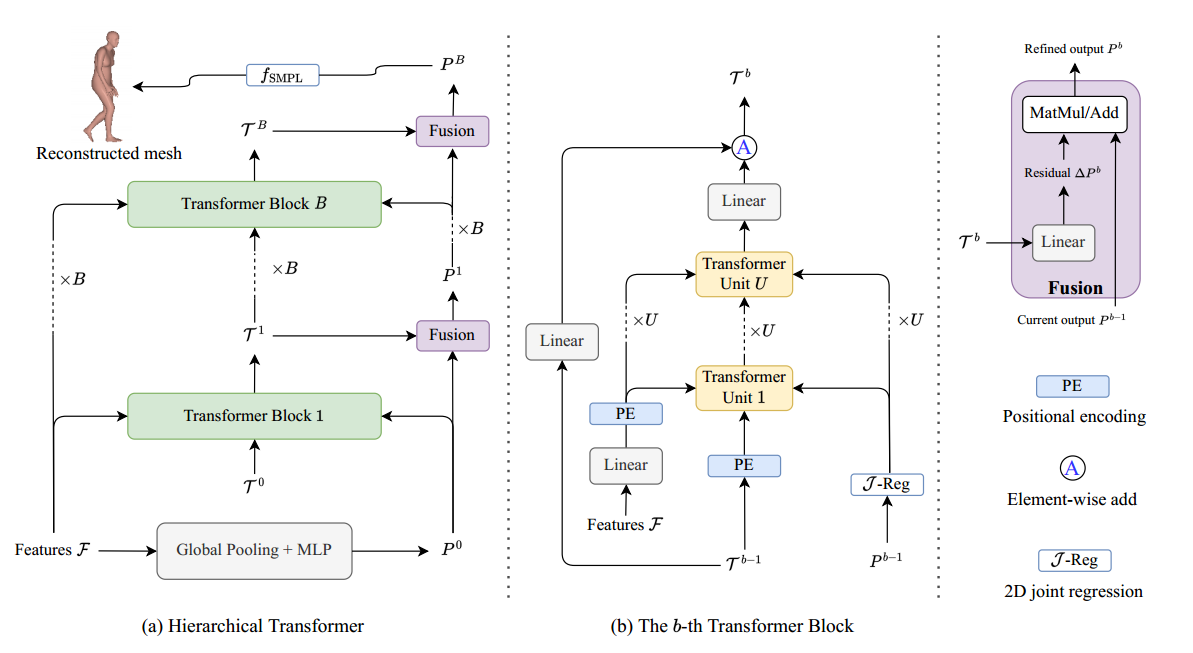
把b阶段的结果写作$P^b = {R_{\theta_1}^b,…,R_{\theta_H}^b, \beta^b, C^b }$,迭代过程:
$\mathcal{T}^b = f_{TB}^b (\mathcal{T}^{b-1} , P^{b-1}, \mathcal{F})$
$P^b = f_{fusion}(\mathcal{T}^b, P^{b-1}), b = 1,2,…,B$
初始化操作:$\mathcal{T}0 = f{global}(F_S) + f_{linear}(P^0)$
7. 损失与评价
损失函数
- 顶点坐标损失:$w_Y · ||Y-\hat{Y}||_1$
- 3D关节损失:$w_J · ||J - \hat{J}||_2 $
- 2D关节损失:$w_\mathcal{J} · ||\mathcal{J} - \hat{\mathcal{J}}||_2 $
- 旋转正则化项:$w_R · \frac{1}{H} \sum_{i=1}^{H} ||R_{\theta_i} - \hat{R_{\theta_i}}||_1$
评价
MPJPE(mean per-joint position error):$\frac{1}{H} \sum_{i=1}^{H}||J_i - \hat{J_i}||_2$,易被缩放,旋转,平移等操作影响。
PA-MPJPE(Procrustes-aligned mean per-joint position error):
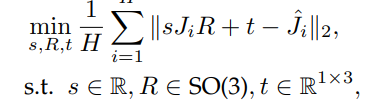
问题
Q1: 什么是SMPL模型?
蒙皮的人体线性模型(参数化人体模型),通过确定关于人体的形状和姿态参数就可以确定这个人体模型使其展现出相应的姿态。我的方法是 通过我的模型能输出SMPL模型的参数 + 相机参数从而得到人体mesh的各个顶点的坐标,通过通过线性投影能得到3D关节坐标,3D关节坐标+相机参数投影能得到2D坐标