深度生成模型
深度生成模型
生成模型
机器学习的两种范式
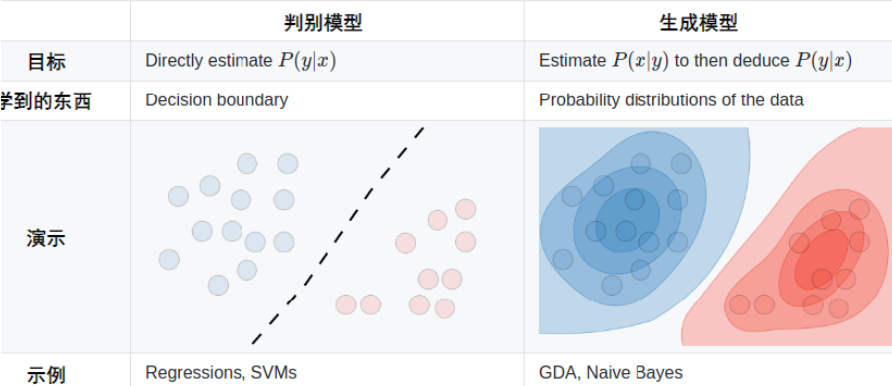
生成模型:用于随机生成可观测数据的模型,是一种密度估计问题。
包括两个步骤:
- 密度估计:分显式密度估计(明确定义模型,直接从样本来估计概率分布)和隐式密度估计(通过拟合模型,使其能够生成符合数据分布的样本)。
- 采样
深度生成模型:
变分自编码器
自编码器
对一组$D$维的样本$x^n \in R^D, 1 \leq n \leq N$,自编码器将这组数据样本映射到特征空间,得到样本的编码$z^n \in R^M$。每个样本都有对应的一个编码, 并且通过这组编码可以重构出原来的样本集合。
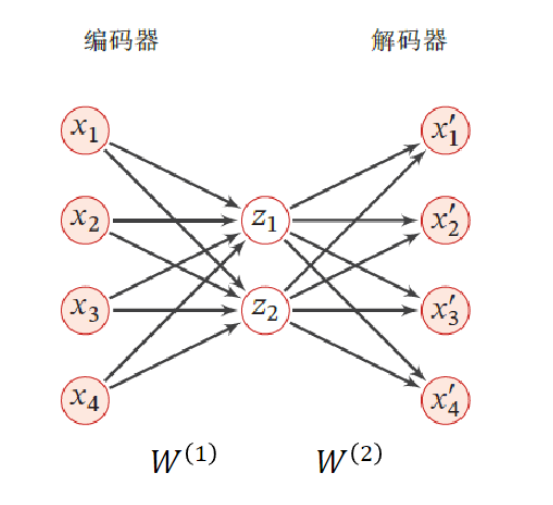
自编码器的结构可分为两部分:
(1) 编码器(Encoder)$f: R^D \rightarrow R^M $ $z = f(W^1x + b^1)$
(2) 解码器(Decoder)$g:R^M \rightarrow R^D$ $x^{‘} = g(W^2z + b^2)$
优化目标: $L = \sum_{n =1}^N ||x^{(n)} - x^{‘(n)}||^2$
· 如果特征空间的维度$M$小于原始空间的维度$D$,自编码器相当于是一种降维或者特征提取的方法。
· 如果令$W^2$等于$W^1$的转置,则称为捆绑权重。捆绑权重自编码器的参数更少,因此更容易学习,且捆绑权重还在一定程度上起到正则化的作用。
变分自编码器
变分自编码器是一种深度生成模型,其思想是利用神经网络来分别建模两个复杂的条件概率密度函数。
用神经网络来估计概率分布$q(z|x;\phi )$称为推断网络$f_I(x;\phi)$。 推断网络输入为$x$,输出为概率分布$q(z|x;\phi)$
用神经网络来估计概率分布$p(x|z;\phi)$称为生成网络$f_G(z;\theta)$。生成网络输入为$z$,输出为概率分布$p(x|z;\theta)$
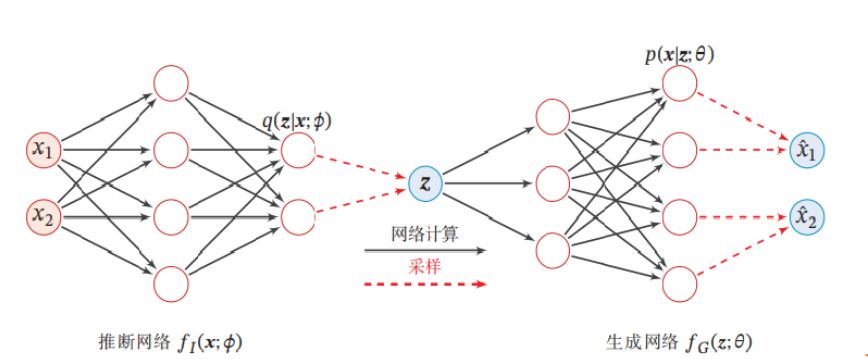
VAE和AE的区别
- AE的隐变量服从的分布未知,而VAE中的隐变量是假设服从某种分布的(如高斯分布)
- AE的编码器输出为确定的编码,而VAE的编码器和编码器的输出为分布(或分布的参数)
- AE智能从一个$x$,重构出相对应的$\hat{x}$,而VAE可以采样生成新的$z$,从而得到新的$\hat{x}$,即产生不同的新样本
生成对抗网络(GAN)
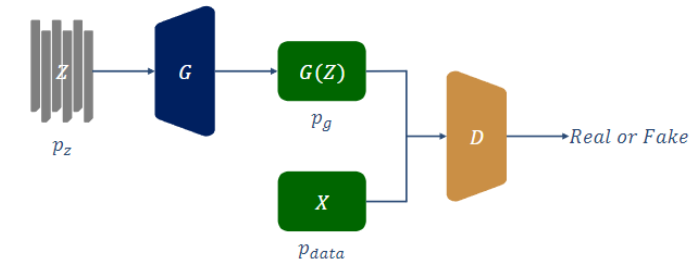
$Z$ : 服从$p_z$分布的样本集($p_z$为预先自定义的分布)
$G$:生成器(三层BP网络)——>模仿原始数据集的分布$p_{data}$
$G(Z)$:生成器的输出
$p_g$:生成器的分布
$X$:原始数据集
$p_{data}$:原始数据集的分布
$D$:判别器(三层BP网络)——>判别输入来自与$p_g$还是$p_{data}$
生成器最大化其对$p_{data}$的模仿能力
判别器最大化其对数据是来与$p_g$还是$p_{data}$的判别能力
目标函数: $\underset{G}{\min} \underset{D}{\max} V(G,D) = E_{x ~p_{data}(x)}[log(D(X))] + E_{z ~p_{z}(z)}[1- log(D(G(z)))]$
$D($ * $)$是判别器输出,标量,即样本*自于$p_{data}$而不是$p_g$的概率
生成器最大化其对$p_{data}$的模仿能力,即最小化$log(1- D(G(z)))$
算法:

for i in 1…n do: (把上述算法的k取1)
Step1: 从噪声中采样输入生成器生成出样本${z^{(1)}, z^{(2)},.., z^{(m)}}$
**Step2:**从真实样本中采样生成样本${x^{(1)}, x^{(2)},…,x^{(m)}}$
**Step3:**根据目标函数计算器损失,求梯度$\triangledown_{\theta_d} \frac{1}{m} \sum_{i=1}^{m} [logD(x^{(i)}) + log(1 - D(G(z^{(i)})))]$,更新判别器的参数$\theta_d$
**Step4:**再从噪声中采样输入生成器生成出样本${z^{(1)}, z^{(2)},.., z^{(m)}}$
**Step5:**计算生成器的梯度$\triangledown_{\theta_g} \frac{1}{m} \sum_{i=1}^{m} [log(1 - D(G(z^{(i)})))]$,更新生成器的参数$\theta_g$
end for 判别器收敛即可(判别器无法区分输入样本是来自于生成器还是原始数据集)
重点
掌握什么是生成模型,以及机器学习的两大范式
自编码器和变分自编码器的结构
GAN的结构以及算法