网络优化与正则化
网络优化与正则化
网络优化
网络优化的难点:
- 不同网络的结构差异大,没有通用的优化算法,超参数多
- 非凸优化问题,如何继续参数初始化和逃离局部最优
- 梯度消失和梯度爆炸问题
网络优化的方法
梯度下降法(GD)
批量梯度下降法(BGD)
批量梯度下降得到的是一个所有训练数据上的全局最优解,每一次的参数更新都用到了所有的训练数据,如果训练数据非常多的话,执行效率较低。
$\theta_j^{‘} = \theta_j + \frac{1}{m}\sum_{i=1}^{m}(y^i - h_\theta(x^i))x_j^i$
缺点:处理大型数据缓慢,易导致内存溢出; 更新快慢由学习率决定,在非凸曲面中可能会趋于局部最优;
随机梯度下降法(SGD)
利用单个样本的损失函数对θ求偏导得到对应的梯度,来更新θ
$\theta_j^{‘} = \theta_j + (y^i - h_\theta(x^i))x_j^i$
缺点:噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向,; 当数据较多时,训练缓慢。
小批量梯度下降法(Mini-Batch GD)
利用部分样本的损失函数对θ求偏导得到对应的梯度,来更新θ
for k = 1, 11, 21, ..,,99 do
$\theta_j^{‘} = \theta_j + \frac{1}{10}\sum_{i=k}^{k+9}(y^i - h_\theta(x^i))x_j^i$
优点:能减少参数更新的波动,获得更好和更稳定的收敛

优化方法:
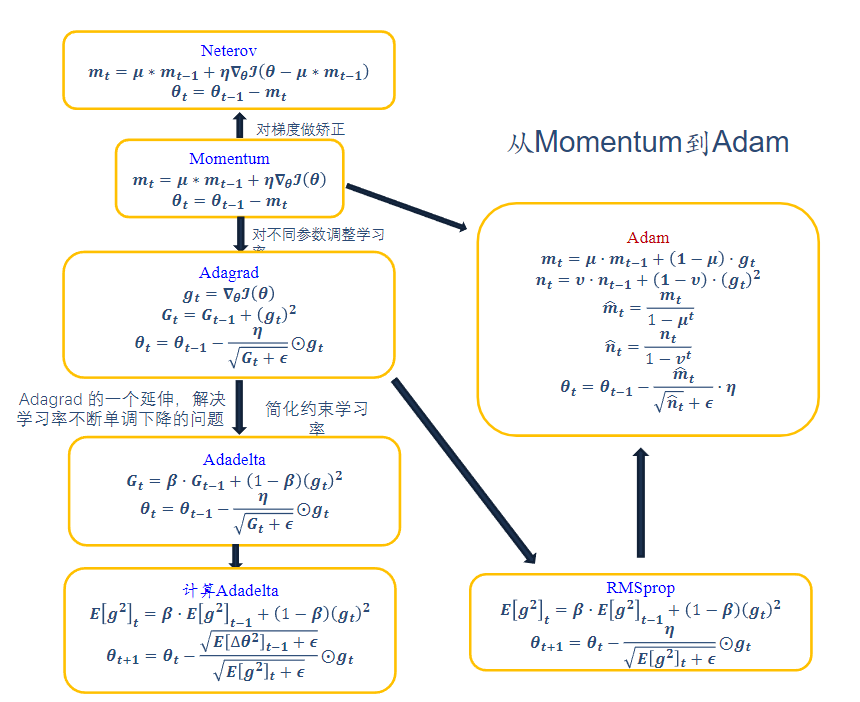
网络优化与正则化
https://wendyflv.github.io/2024/06/09/网络优化与正则化/