循环神经网络
循环神经网络
递归神经网络RNN
RNN按照时间序列展开:
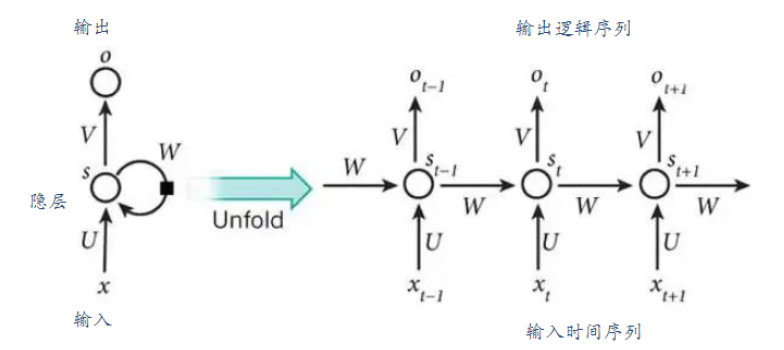
正向传播
$t$时刻中间隐层输入$s_t = Ux_t + Wh_{t-1}$
$t$时刻中间隐层输出$h_t = f(s_t)$(其中$f$为sigmoid函数)
$t$时刻输出层输出$o_t = g(Vh_t)$(其中$g$为softmax函数)
损失函数为$L_t = -[y_tlogo_t + (1-y_t)log(1-o_t)]$
所有时间的损失为$L = sum_{t=1}^{T}L_t$
反向传播
首先对$V$求导,直接得到:
$\frac{\partial L}{\partial V} = \sum_{t=1}^T \frac{\partial L_t}{\partial V} = \sum_{t=1}^{T} \frac{\partial L_t}{\partial o_t} \frac{\partial o_t}{\partial V} = \sum_{t=1}^{T} -(\frac{y_t}{o_t} + \frac{y_t-1}{1-o_t}o_t(1-o_t)h_t^T) = \sum_{t=1}^{T} (o_t - y_t)h_t^T$
对$W$求梯度,
$\frac{\partial L}{\partial W} = \sum_{t=1}^T \frac{\partial L_t}{\partial W} =\sum_{t=1}^T \frac{\partial L_t}{\partial o_t} \sum_{k=1}^t \frac{\partial o_t}{\partial h_t} \frac{\partial h_t}{\partial h_k} \frac{\partial h_k}{\partial W} = \sum_{t=1}^T \sum_{k=1}^t \frac{\partial L_t}{\partial o_t}\frac{\partial o_t}{\partial h_t}(\prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}})\frac{\partial h_k}{\partial W} $
依此类推出:
$\frac{\partial L}{\partial U} = \sum_{t=1}^T \sum_{k=1}^t \frac{\partial L_t}{\partial o_t}\frac{\partial o_t}{\partial h_t}(\prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}})\frac{\partial h_k}{\partial U} $
弊端
传统RNN都采用反向传播时间算法(BPTT),随着时间流逝,网络层数增加,会产生梯度消失或者梯度爆炸的问题。
以$W$的梯度更新举例,使用激活函数假如是$tanh$
$\frac{\partial h_j}{\partial h_{j-1}} = W^T \odot tanh^{‘}, tanh^{‘} \in [0,1]$
👉梯度消失:如果$W$也是大于0小于1的数,当$t$很大时,$W^T \odot tanh^{‘} <1 $,连乘起来就会趋于0.
👉梯度爆炸:如果梯度比较大的话($\frac{\partial h_j}{\partial h_{j-1}} > 1$),经过多层迭代,又会导致梯度大的不得了,比如$1,01^{100}$。
梯度消失和爆炸实际上导致了网络只能学习到短周期的依赖关系。
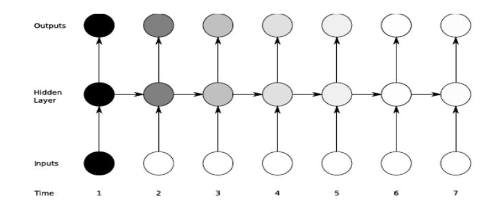
随着时间的推移,对于 t>1 时刻的产生的影响会越来越小,由图中的颜色的深浅代表信号的大小。这种衰减会导致 RNN 无法处理长期依赖。
LSTM(长短时记忆神经网络Long short-term memory)
与RNN的区别
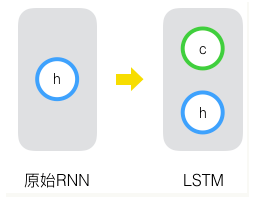
· 原始RNN的隐藏层只有一个状态,即$h$,它对于短期输入非常敏感
· 再增加一个状态$c$,来保存长期的状态,称为单元状态或者内部记忆单元,记录了当前时刻为止的所有历史信息。
内部记忆单元C
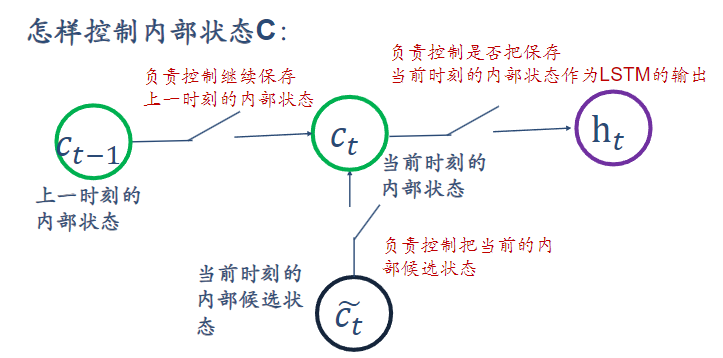
第一个开关,负责控制继续保存内部状态C(遗忘门)
遗忘门可以保存很久很久之前的信息
它决定了上一时刻的单元内部状态$c_{t-1}$有多少保留到当前内部时刻内部状态$c_t$
第二个开关,负责控制把当前内部候选状态输入到当前状态C(输入门)
它决定了当前时刻网络的输入$x_t$有多少保存到当前单元内部状态$c_t$
第三个开关,负责控制是否把内部状态C作为当前LSTM的输出(输出门)
它决定了内部状态$c_t$有多少输出到LSTM的当前输出值$h_t$
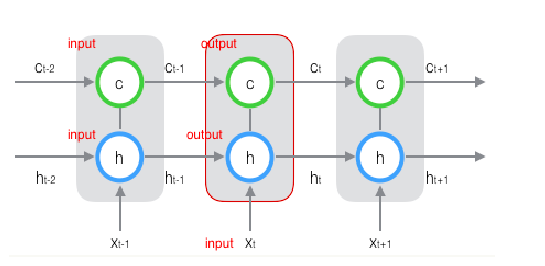
核心思想:LSTM的关键在于细胞的状态整个(绿色的图表示的是一个cell),和穿过细胞的那条水平线。
细胞状态类似于传送带。直接在整个链上运行,只有一些少量的线性交互。信息在上面流传保持不变会很容易。
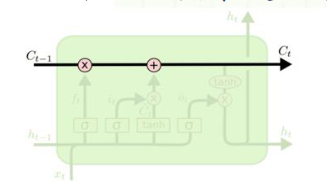
若只有上面的那条水平线是没办法实现添加或者删除信息的。而是通过一种叫做 门(gates) 的结构来实现的。
门可以实现选择性地让信息通过,主要是通过一个 sigmoid 的神经层 和一个逐点相乘的操作来实现的。
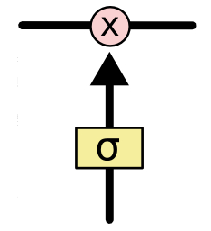
LSTM的3个门
遗忘门(控制内部记忆单元遗忘哪些历史信息)$f_t$
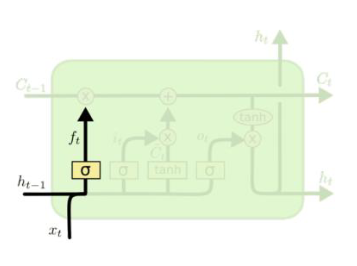
$f^t = \sigma(W_f \cdot h^{t-1} + U_f \cdot x^t + b_f)$
输入门(控制内部记忆单元加入多少新信息)
Part1
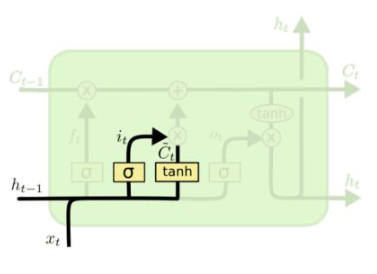
$i^t = \sigma (W_i h^{t-1} + U_ix^t + b_i)$
$\tilde{c}^t = tanh(W_c h^{t-1} + U_c x^t + b_c)$
Step1: 通过输入门的sigmoid层决定加入哪些新信息
Step2: 再由tanh层通过$X$和$h$值,生成一个候选记忆向量。
Part2
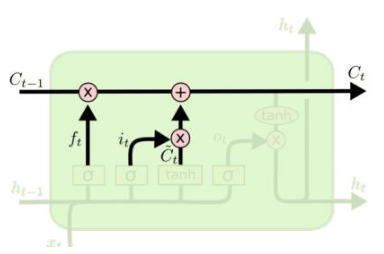
$c^t = f^t * c^{t-1} + i^t * \tilde{c}^t$
新的内部记忆单元包括两部分
1 经过遗忘门过滤的旧状态信息
2 候选记忆向量与通过输入门决定的 $𝑖^𝑡$的乘积输出门
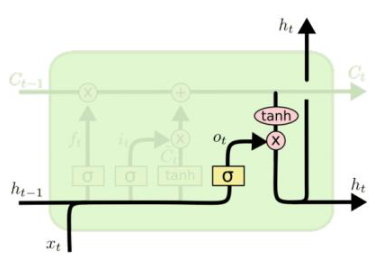
$o^t = \sigma(W_o h^{t-1} + U_o x^t + b_o)$
$h^t = o^t * tanh(c^t)$
$c^t$通过tanh函数,将输出信息控制在-1到1之间。
总结:
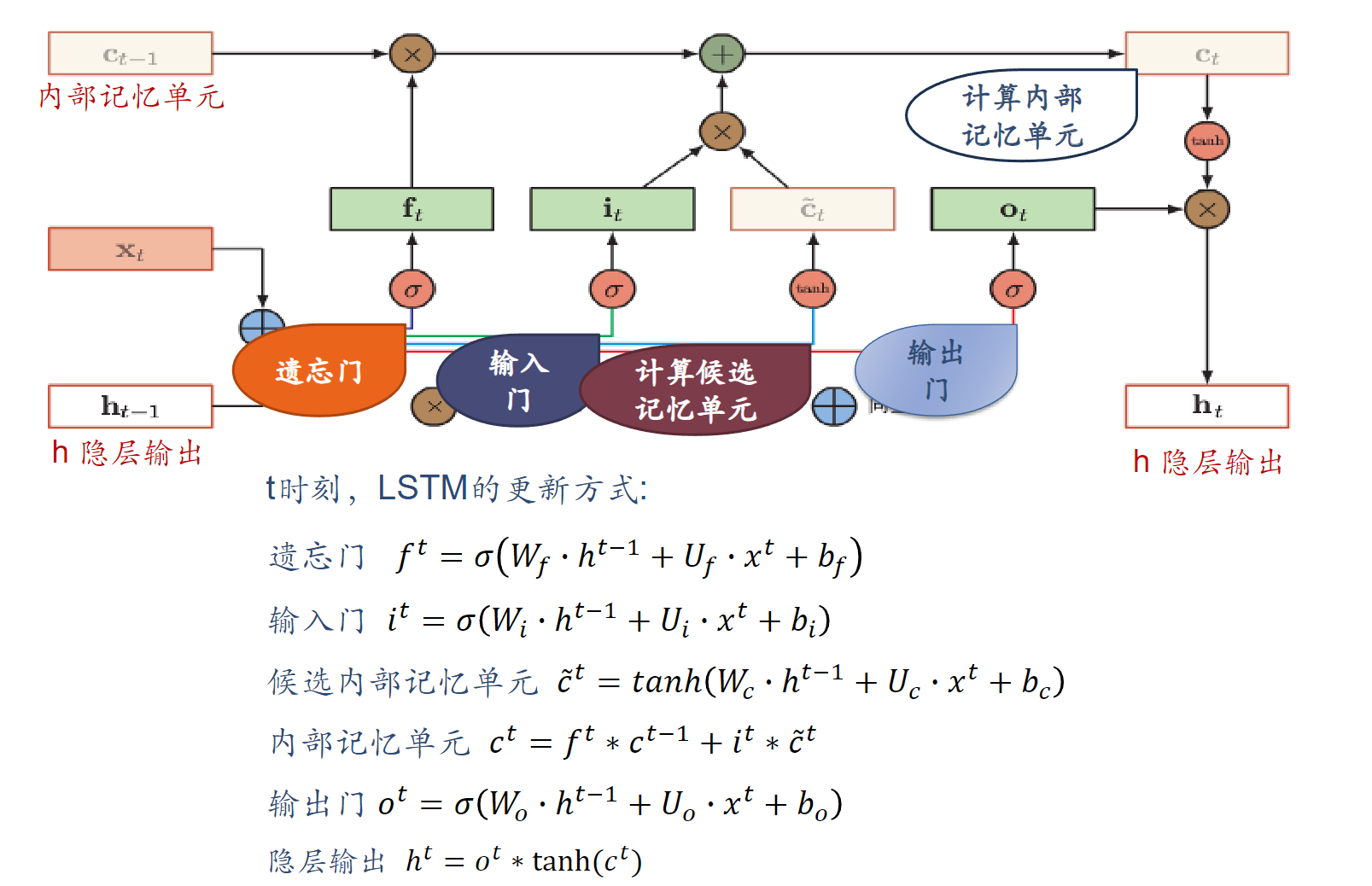
缓解梯度消失和爆炸
由正向传播公式:$c^t = f^t * c^{t-1} + i^t * \tilde{c}^t$
得到 $\frac{\partial c^{t+1}}{\partial c^t} = f^t + …$
可以看到当$f^t =1$时,就算其余项很小,梯度仍可以很好的导到上一时刻,此时即使层数较沈也不会发生梯度消失;当$f^t = 0$时,即上一时刻的信号不影响当前时刻,梯度也不会传回去。
训练过程
误差使用交叉熵函数
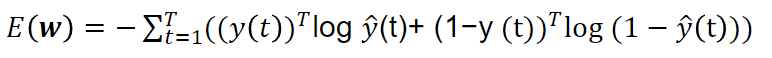
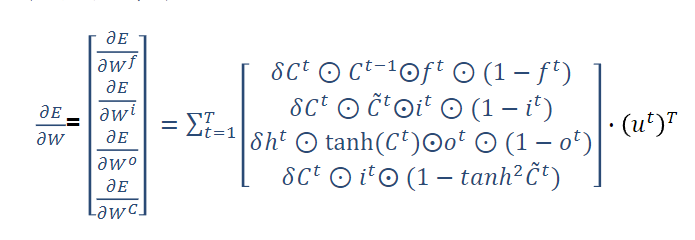
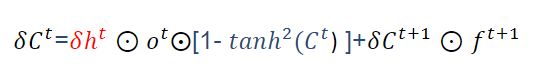
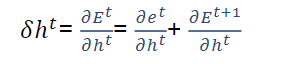
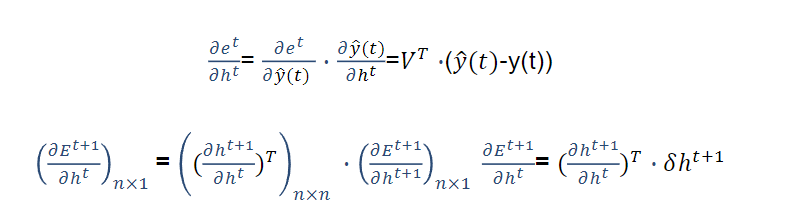

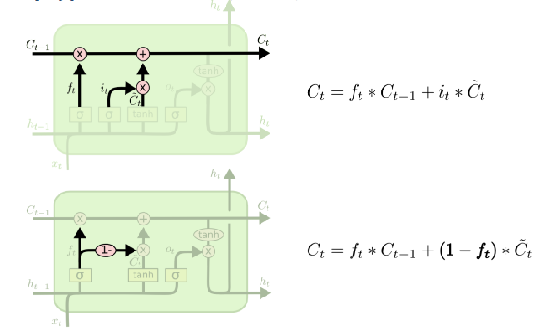
LSTM其他变体
合并遗忘门和输入门 $i_t + f_t$ =1
GRU
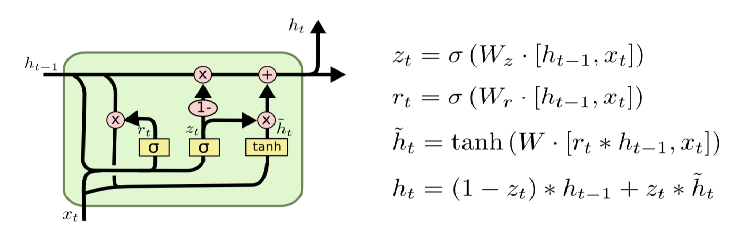
GRU只有两个门:更新门z和重置门r
更新门:遗忘多少历史信息和接受多少新信息。
重置门:候选状态中有多少信息是从历史信息中得到的。
与LSTM的比较:
- GRU少了一个门,也少了一个细胞状态$c_t$
- GRU只需要重置门来控制是否要保留原来隐藏状态的信息,单步在限制当前信息的传入。
- 在 LSTM 中,虽然得到了新的细胞状态$ 𝒄_𝒕$,但是还不能直接输出,而是需要经过一个过滤的处理:;同样,在GRU 中, 虽然我们也得到了新的隐藏状态$\tilde{h}_t$, 但是还不能直接输出,而是通过更新门来控制最后的输出。
重点
- RNN构造
- RNN的梯度消失和梯度爆炸产生原因
- LSTM结构及核心思想