卷积神经网络
卷积神经网络
卷积
卷积经常用在信号处理中，用于计算信号的延迟累积。
一维卷积
时刻t收到的信号$y_t$ 为当前时刻产生的信息和以前时刻延迟信息的叠加: $y_t = 1 \times x_t + 1/2 \times x_{t-1} + 1/4 \times x_{t-2}= w_1x_t + w_2x_{t-1}+w_3 x_{t-2} = \sum_{k=1}^{3}w_k x_{t-k+1}$
$w_k$称为滤波器或者卷积核
给定一个输入信号序列$x$和滤波器$w$，卷积的输出：$y_t = \sum_{k=1}^K w_k x_{t-k+1}$
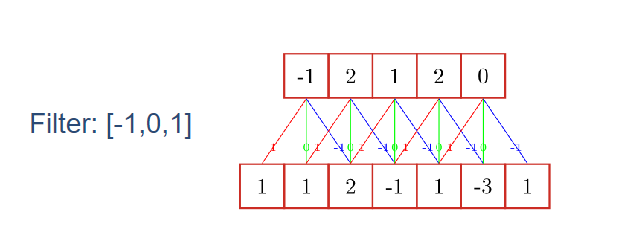
不同的滤波器来提取信号序列中的不同特性
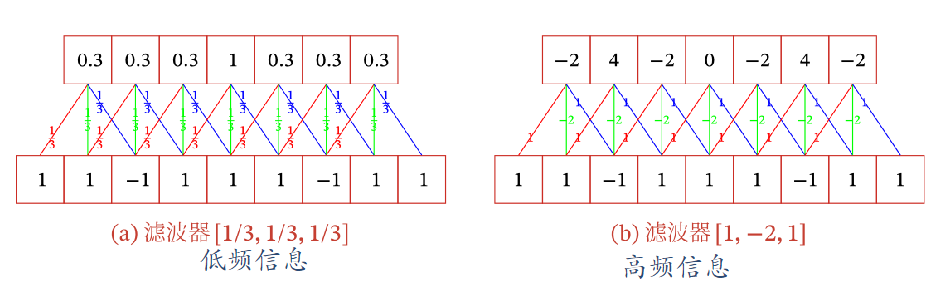
👉低通滤波：滤波器$[1/3, 1/3, 1/3]$可以检测信号序列中的低频信息（如均值）
👉高通滤波：滤波器$[1, -2, 1]$可以检测信号中的高频信息（如边缘）
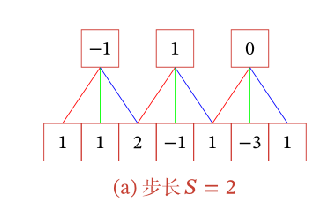
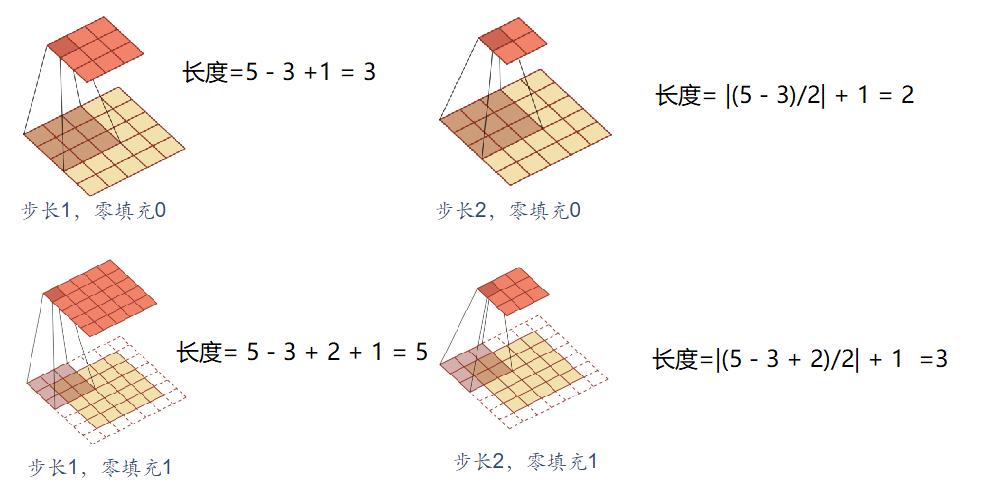
引入滑动步长$S$和零填充$P$:
$S=2$即卷积核每隔2步做一次卷积运算
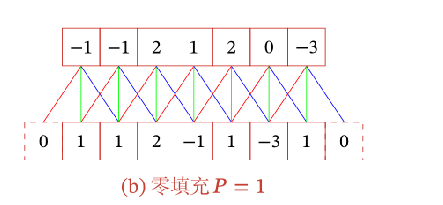
$P=1$即原数据左右两边各填充一个0（避免重要信息的丢失）
卷积类型：按照输出长度可分为3类
$M$为输入序列的长度，$K$为窗口大小
- 宽卷积：步长$S=1$，两边不补零$P=0$，卷积后输出长度为$M-K+1$
- 窄卷积：步长$S=1$，两边补零$P=K-1$，卷积输出长度为$M+K-1$
- 等宽卷积：步长$S=1$，两端补零$P=(K-1)/2$，卷积后输出长度为$M$
对一个步长为$S$，填充为$P$的卷积，输出的长度为：$|\frac{M+2P-K}{S}| + 1$
二维卷积
在图像处理中，图像是以二维矩阵的形式输入到神经网络中，因此我们需要二维卷积。
一个输入信息$X$和滤波器$W$的二维卷积定义为：$Y=W * X$
$y_{ij} = \sum_{u=1}^{U}\sum_{v=1}^{V} w_{uv}x_{i-u+1, j-v+1}$
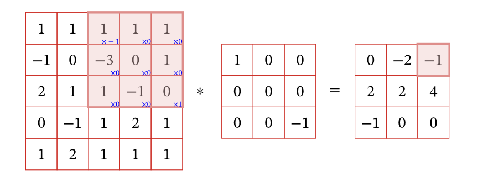
步长和填充不同的情况：
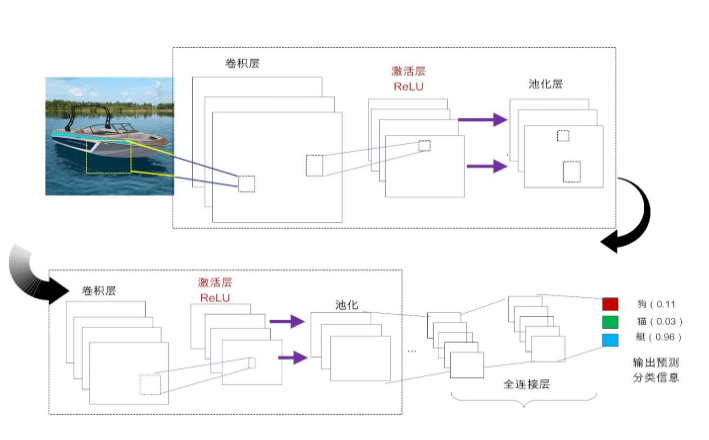
卷积神经网络
网络结构：
👉数据输入层（Input layer）
- 局部特征提取
- 训练中参数学习
- 每个卷积核提取特定模式的特征
👉ReLU激励层（ReLU layer）
- 降低数据维度，避免过拟合
- 增强局部感受野
- 提高平移不变性
👉全连接层（FC layer）：特征提取到分类的桥梁
卷积层
卷积代替全连接层 $h^{l+1} = f(w * h^l + b)$
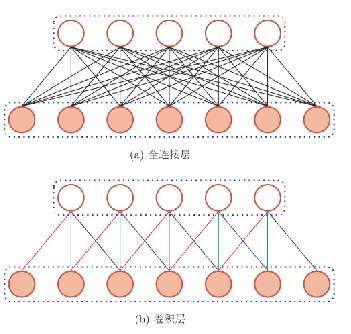局部连接，权重共享，空间或者时间上的次采样
卷积与协相关：
协相关：核核输入数据对应相乘再求和
卷积：核先翻转180度，再做协相关
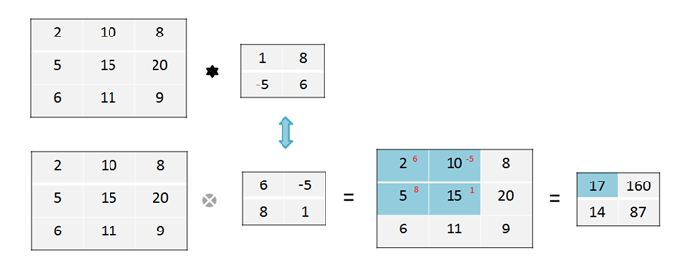
除非特殊声明，计算结果按照协相关来。
多个卷积核：使用多个卷积核能增强卷积层的提取不同特征的能力
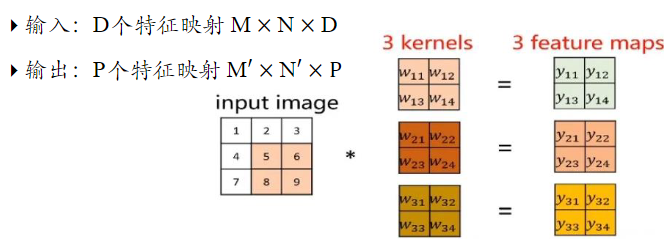
输入$[7 \times 7 \times3] \rightarrow $ 经过卷积核$w_0[3 \times 3 \times 3]+b_0, w_1[3 \times 3 \times 3]+b_1 \rightarrow$ 结果$[3 \times 3 \times 2]$
(两个卷积核的大小必须一致)
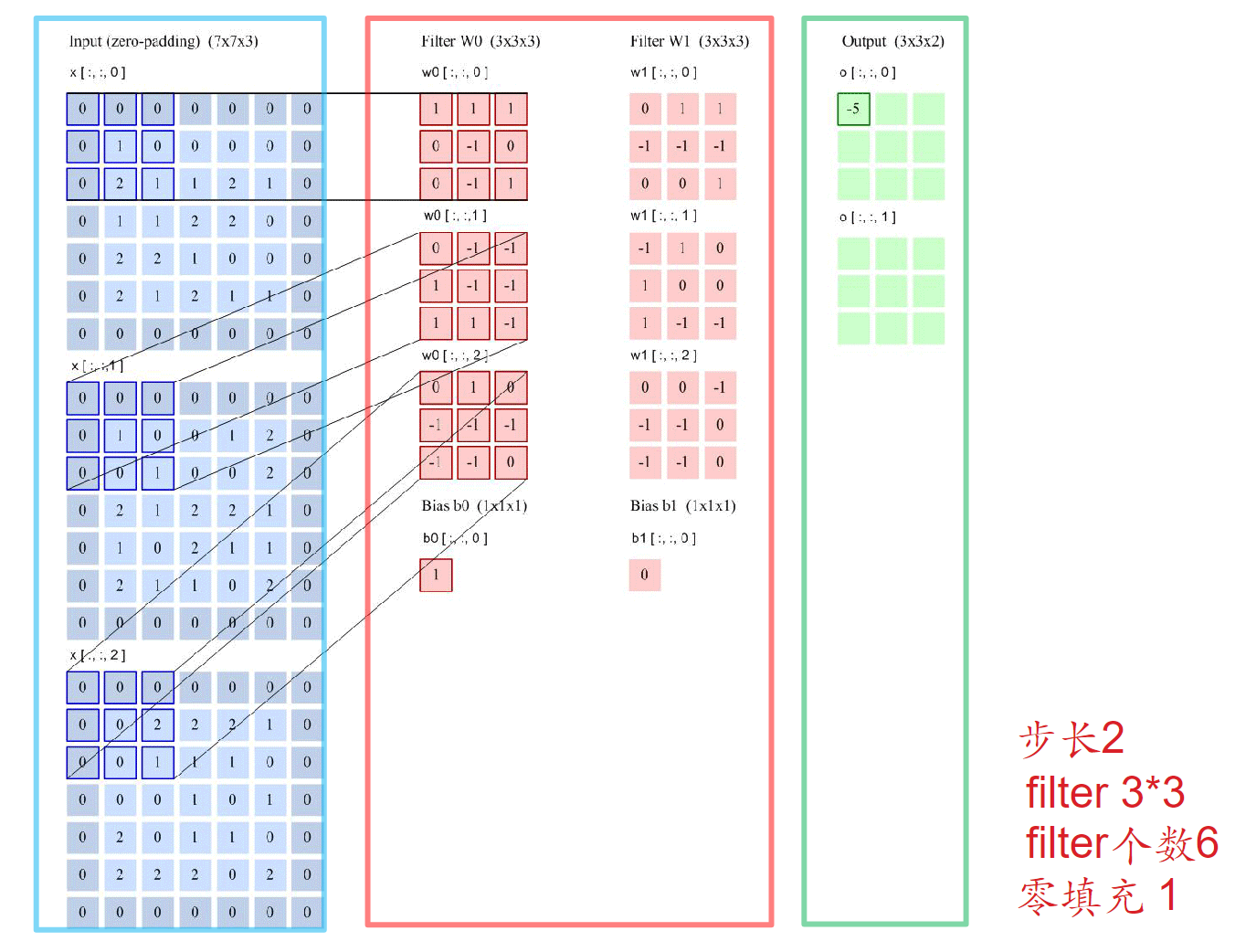
3通道图像的卷积层：经过多少个卷积核，就会产生多少通道特征图
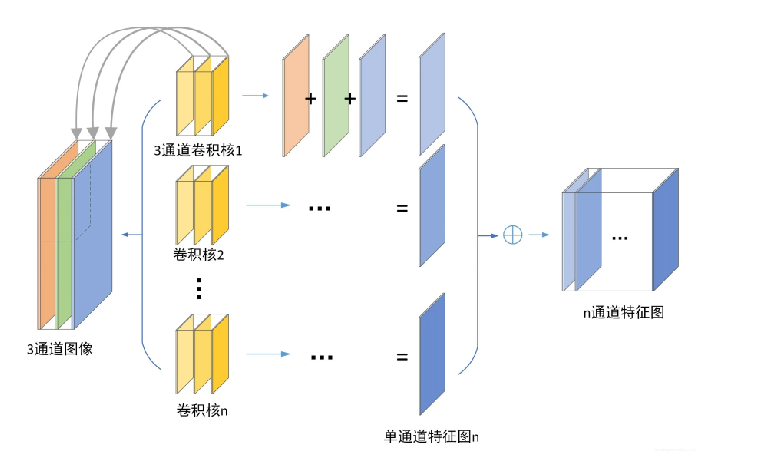
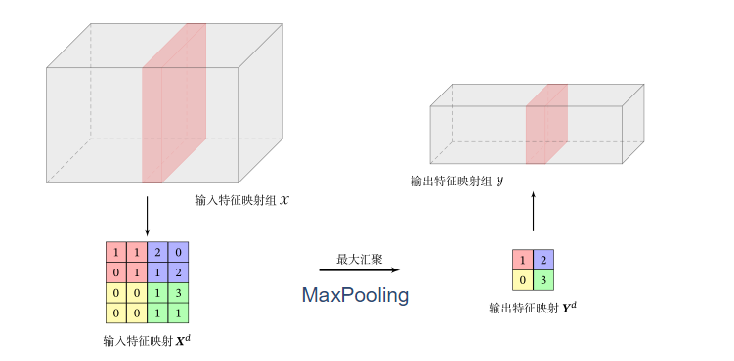
池化层或汇聚层（Pooling Layers）
卷积层虽然可以显著减少连接的个数，但是每一个特征映射的神经元个数并没有显著减少。
下面是最大池化是的作用方式：
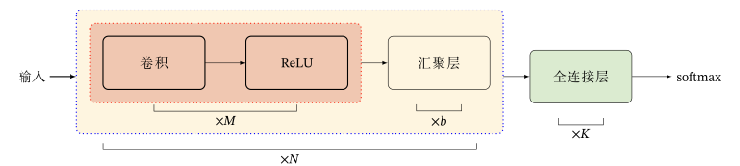
卷积网络是由卷积层、汇聚层、全连接层交叉堆叠而成的
经典结构如下：一个卷积块为连续$M$个卷积层和$b$个汇聚层。一个卷积网络可以堆叠$N$个连续的卷积块，然后在接着$K$个全连接层。
误差反向传播
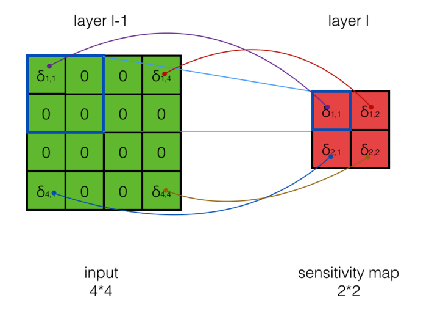
卷积层的反向传播
- 误差的传播
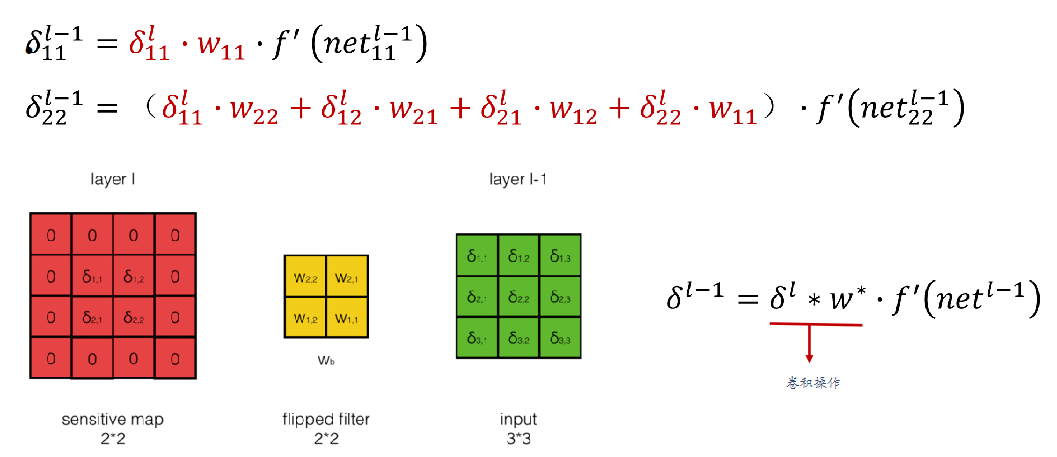
权重梯度的计算
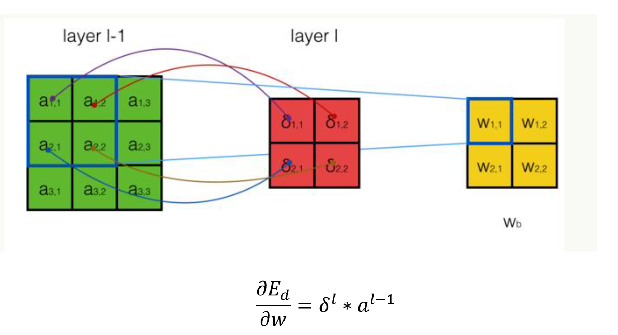
池化层的反向传播
误差的传播
对最大池化，下一层的误差项会原封不动的传给上一层对应区块的最大值所对应的神经元，而其他神经元的误差项都是0。（平均池化就是每个误差项系数为1/K）
其他卷积种类
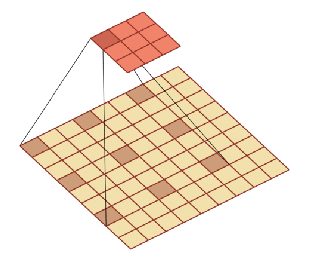
空洞卷积
通过给卷积核插入“空洞”来变相地增加其大小，以增加输出单元的感受野
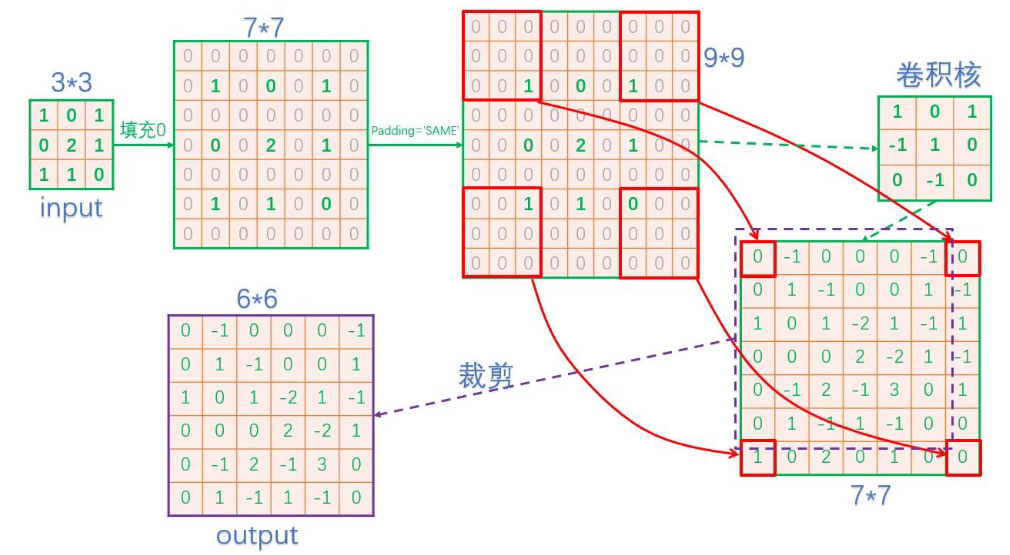
转置卷积/微步卷积
可分离卷积
👉空间可分离卷积
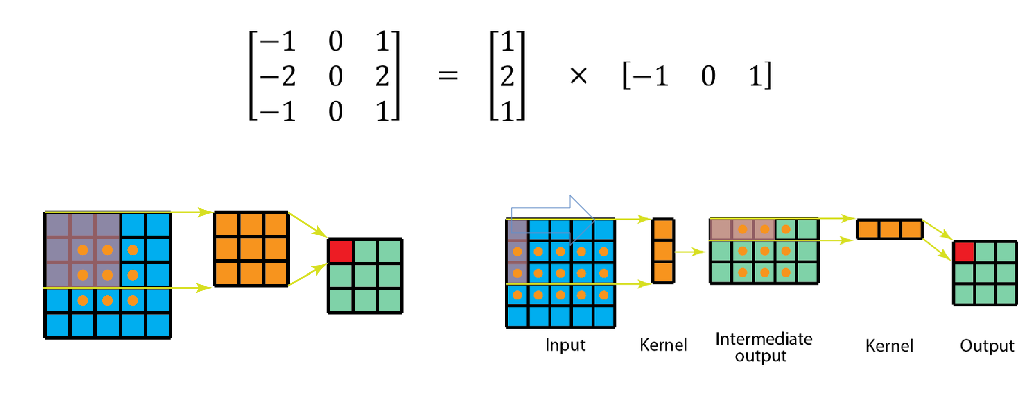
👉深度可分离卷积
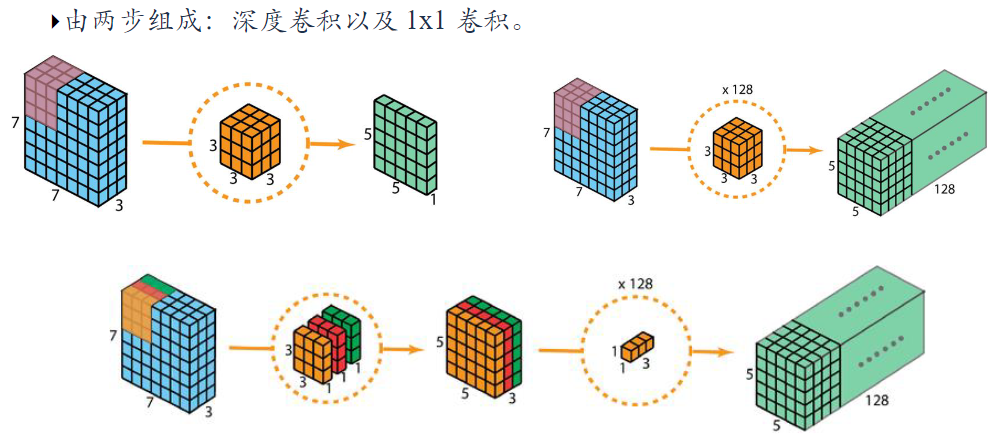
经典卷积网络
残差网络
残差网络（Residual Network，ResNet）是通过给非线性的卷积层增加直连边的方式来提高信息的传播效率。
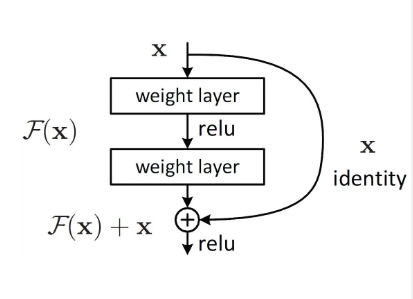
好处：
- 能够解决梯度消失问题，适用于深层结构。
- 加速了模型训练收敛速度，使得模型更容易地学习到恒等映射（identity mapping）或者近似于恒等映射的变换。
- 即学习输入与目标之间的差异，而不是直接学习输出。这样的设计使得网络可以更好地适应复杂的数据分布，提高了网络的表达能力
CNN的优缺点
优点：
- 共享卷积核，对高维数据处理无压力
- 无需手动提取特征，训练好合适的权重，可以获取好的特征
- 分类效果好
缺点：
- 需要调参，还需要大样本，训练要GPU
- 物理含义不明确
重点
- 卷积网络的三个结构特征：共享权值，局部连接，时间或空间上的次采样
- 卷积的定义，以及各式各样的卷积
- 卷积网络结构（卷积块的构成+全连接层）
- 理解残差网络的机理