前馈神经网络
前馈神经网络
感知机模型
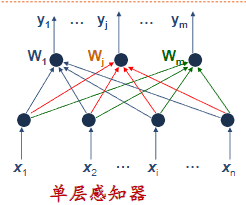
单层感知机
输入层:感知层,n个神经节点,无信息处理能力,只负责引入外部信息X。
处理层:m个神经接点,每节点均有信息处理能力,m个节点向外部处理输出信息,构成输出列向量Y。
两层间连接权值用权值列向量$W_j$表示,m个权向量构成单层感知器的权值矩阵W。
$W_j=[w_{1j} w_{2j} …w{ij}…w_{nj}]^T $
离散型单计算层感知器采用符号型转移函数,则j节点输出为:
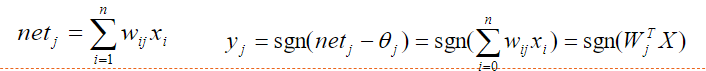
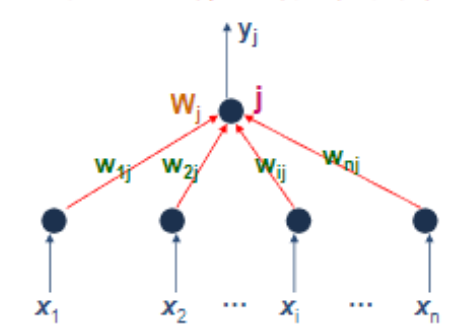
单计算节点感知机
单计算节点感知器实际上就是一个M-P神经元模型。
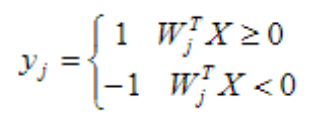
功能:
输入向量$X=[x_1 x_2 …x_n]^T$,则n个输入分量构成几何n维空间,
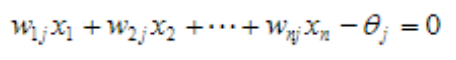
该超平面将样本分成2类。
一个简单的单计算节点感知器具有分类功能,其分类原理是将分类知识存储于感知器的权向量(包括阈值)中,由权向量确定的分类判决界面(线),可将输入模式分为两类。
举例:
功能”与“
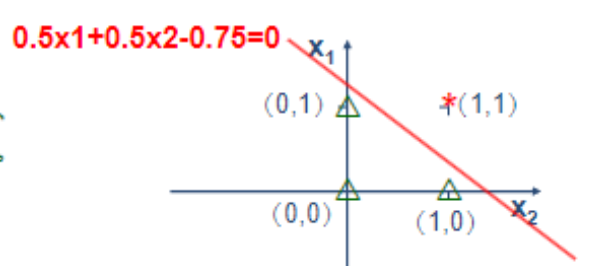
功能”或“
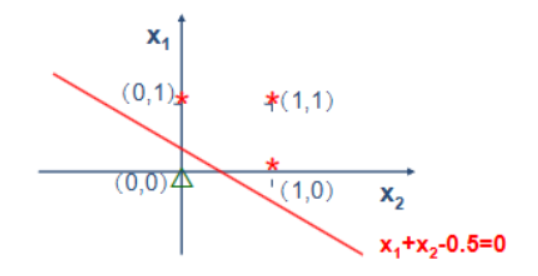
功能”异或”
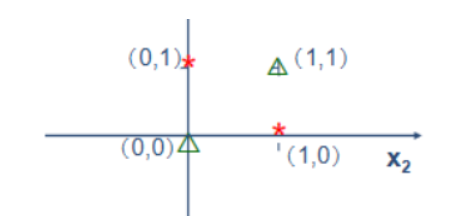
确定的分类判决方程是线性方程,因而只能解决线性可分问题的分类,不能解决线性不可分问题.
这称为单计算层感知器的局限性.
多层感知机
单计算层感知器只能解决线性可分问题,多层感知器可解决线性不可分问题。
输出层节点以隐层两节点y1,y2的输出作为输入,其结构也相当于一个符号单元。
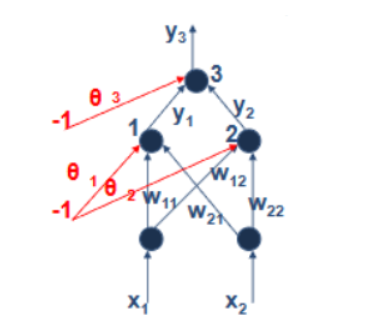
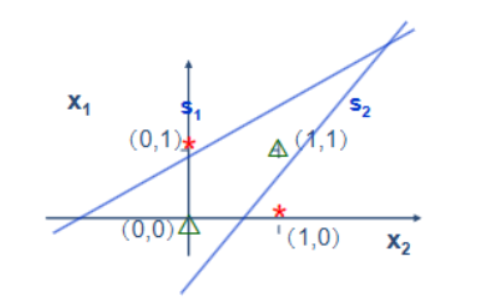
1、2两符号单元确定两条分界直线s1和s2,可构成开放式凸域。
双隐层感知器足以解决任何复杂分类问题,为提高感知器分类能力,可采用非线性连续函数作为神经元节点的转移函数,使区域边界变成曲线,可形成连续光滑曲线域。
神经元
单个神经细胞只有两种状态:兴奋和抑制
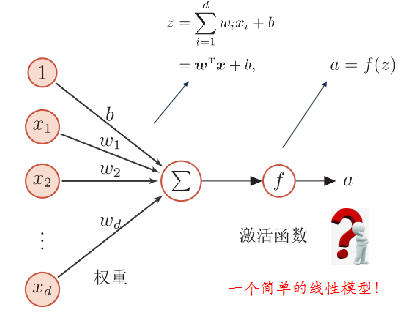
激活函数
· 激活函数的性质:
- 连续并可导的非线性函数(允许在少数点上不可导)
- 激活函数及其导数要尽可能的简单
- 激活函数的导数的值域要在有关合适的区间内
- 单调递增
· 常见的激活函数:
S型
$\sigma(x) = \frac{1}{1+e^{-x}}$
$\tanh(x)=\frac{e^x - e^{-x}}{e^x + e^{-x}} = 2\sigma(2x)-1$
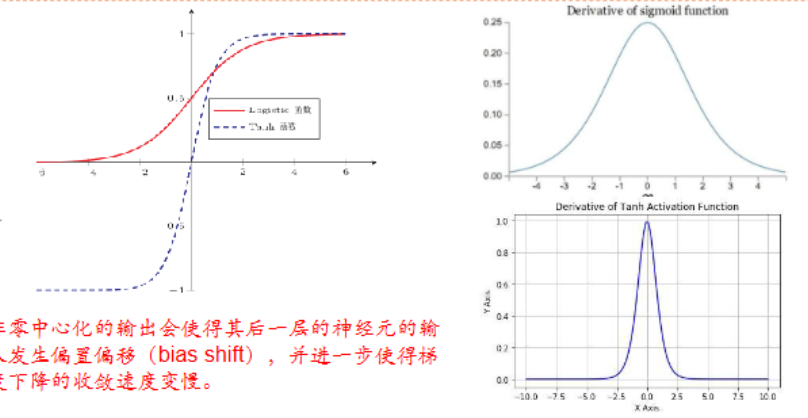
饱和函数:当$x$趋向无穷大时,其导数置趋于0
S型激活函数时饱和函数。(可能会导致梯度消失问题)
Tanh函数时零中心化的,logistic函数的输出恒大于0
斜坡型
$ReLU(x) = \begin{cases} x, & \text{if } x > 0 \ 0, & \text{if } x \leq 0 \end{cases}=max(x,0)$
具有单侧抑制,宽兴奋边界,能在一定程度是缓解梯度消失问题 (ReLU 在正区间(x > 0)上的梯度恒为 1,这意味着在正区间内,梯度不会消失。相比之下,一些传统的激活函数(如 Sigmoid 和 Tanh)在输入值较大或较小时会接近饱和,导致梯度消失,使得网络的训练速度变慢。)
$LeakyReLU(x) = \begin{cases} x, & \text{if } x > 0 \ \gamma x, & \text{if } x \leq 0 \end{cases} = max(0,x) + \gamma min(0,x)$
$PReLU(x) = \begin{cases} x, & \text{if } x > 0 \ \gamma_i x, & \text{if } x \leq 0 \end{cases} = max(0,x) + \gamma_i min(0,x)$
近似零中心化的非线性函数
$ELU(x) = \begin{cases} x, & \text{if } x > 0 \ \gamma (e^x-1), & \text{if } x \leq 0 \end{cases} = max(0,x) + min(0,\gamma(e^x-1))$
ReLU的平滑版本:
$softplus(x) = log(1+e^x)$
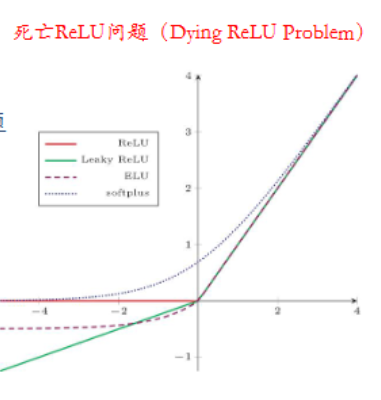
死亡ReLU问题:一些神经元的输出始终为零,导致这些神经元对于网络的训练没有贡献,失去了激活的能力。可使用LeakyReLU缓解
复合函数
自门控激活函数
$swish(x) = x\sigma(\beta x)$
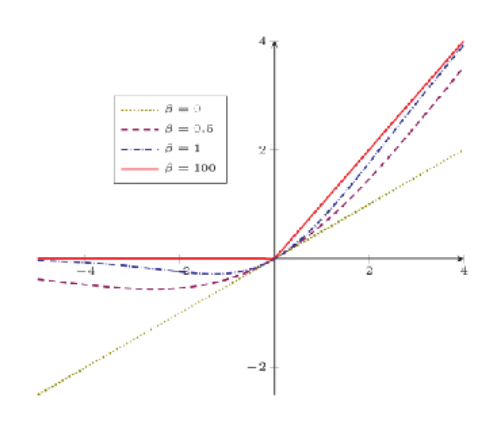
常见激活函数及其导数
| 激活函数 | 函数 | 导数 |
|---|---|---|
| Logistic函数 | $f(x)=\frac{1}{1+e^{-x}}$ | $f^{‘}(x) = f(x)(1-f(x)) $ |
| Tanh函数 | $f(x)=\frac{e^x - e^{-x}}{e^x + e^{-x}}$ | $f^{‘}(x) = 1 - f^2(x)$ |
| ReLU函数 | $f(x) = max(0,x)$ | $f^{‘}(x) = I(x>0)$ |
| ELU函数 | $f(x) = max(0,x)+min(0, \gamma(e^x-1))$ | $f^{‘}(x) = I(x>0) + I(x\leq0)\gamma e^x$ |
| SoftPlus函数 | $f(x) = log(1+ e^x)$ | $f^{‘}(x) = \frac{1}{1+e^{-x}}$ |
人工神经网络
人工神经网络主要由大量的神经元以及它们之间的有向连接构成。
需要考虑三方面:
神经元的激活规则
网络的拓扑结构
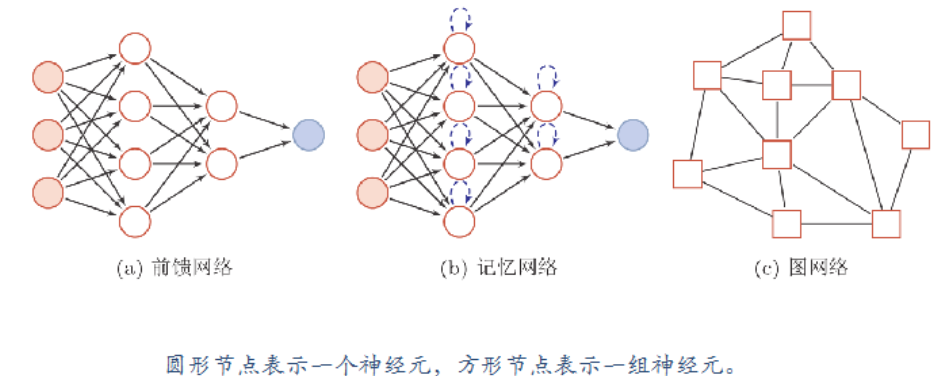
学习算法
前馈神经网络
网络结构
各神经元分别属于不同层,层内无连接
相邻两层之间的神经元全部两两连接
网络中无反馈,信号从输入层想输出层单向传播,可用一个有向无环图表示。
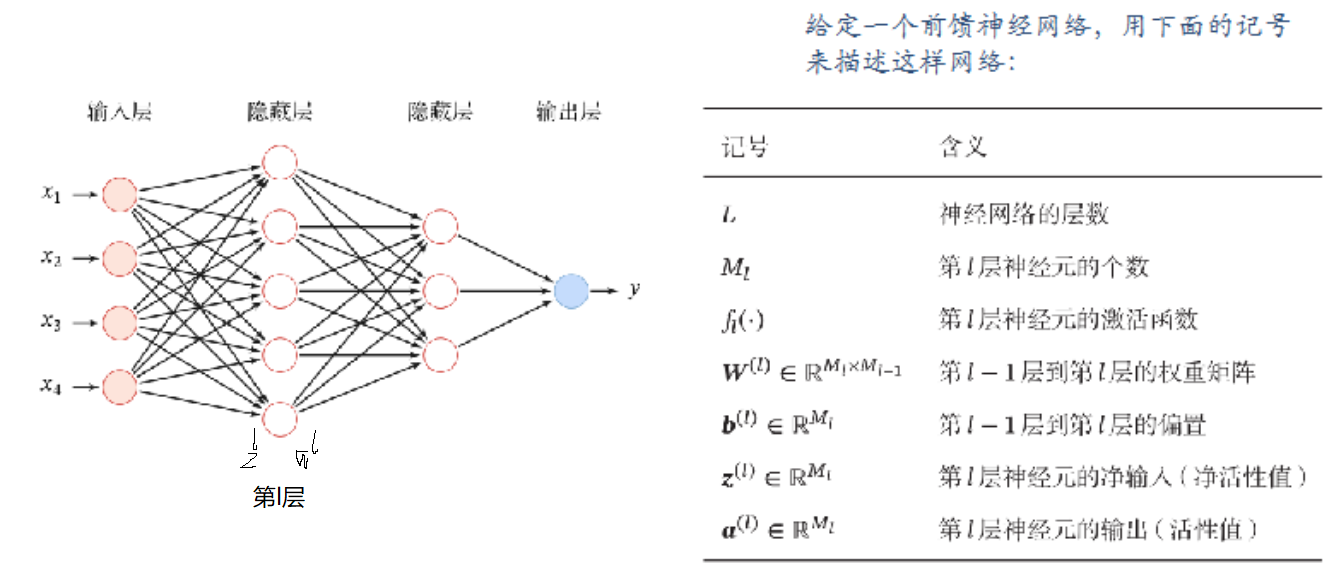
信息传递过程
对第$l$层,其净输入$z^l = W^la^{l-1}+b^l$,其输出为$a^l = f(z^l)$
前馈计算为:$x = a^0 \rightarrow z^1 \rightarrow a^1 \rightarrow z^2 \rightarrow a^{L-1} \rightarrow z^L \rightarrow a^L $
通用近似定理
也叫万能逼近定理
对于具有线性输出层和至少一个使用“挤压”性质的激活函数的隐藏层组成的前馈神经网络,只要其隐藏层神经元的数量足够,它可以以任意的精度来近似任何从一个定义在实数空间中的有界闭集函数。
参数学习
如果使用Softmax回归分类器,相当于网络最后一层设置C 个神经元,其输出经过Softmax函数进行归一化后可以作为每个类的条件概率。
$\hat{y} = softmax(z^L)$
采用交叉熵损失函数,对样本$(x,y)$,其损失函数为:
$L(y,\hat{y}) = -y^Tlog\hat{y}$
给定训练集为$𝐷 = {(𝒙^{(𝑛)}, 𝑦^{(𝑛)} )}_{𝑛=1}^𝑁$ ,将每个样本输入给前馈神经网络,得到网络输出$\hat{𝑦}^{(𝑛)}$ ,其在数据集D上的结构化风险函数为:
$R(W,b) = \frac{1}{N}\sum_{n=1}^{N}L(y^n, \hat{y}^n)+ \frac{1}{2} \lambda ||W||^2$
梯度下降:
$W^l \leftarrow W^l - \alpha\frac{\partial R(W,b)}{\partial W^l} $
$b^l \leftarrow b^l - \alpha\frac{\partial R(W,b)}{\partial b^l} $
反向传播算法
Step1: 顺序表示梯度公式
由公式$z^l = W^la^{l-1}+b^l$得:
$\frac{\partial L(y,\hat{y})}{\partial w_{ij}^l} = \frac{\partial L(y,\hat{y})}{\partial \mathbf{z}^l } \frac{\partial \mathbf{z}^l}{\partial w_{ij}^l} $ , $\frac{\partial L(y,\hat{y})}{\partial \mathbf{b}^l} = \frac{\partial L(y,\hat{y})}{\partial \mathbf{z}^l } \frac{\partial \mathbf{z}^l}{\partial \mathbf{b}^l} $
这里的$\mathbf{z}, \mathbf{b}$都是m维的向量
$\frac{\partial \mathbf{z}^l}{\partial w_{ij}^l} = [ \frac{\partial z^l_1}{\partial w_{ij}^l}, \frac{\partial z^l_2}{\partial w_{ij}^l},…,\frac{\partial z^l_{i}}{\partial w_{ij}^l},…,\frac{\partial z^l_m}{\partial w_{ij}^l}] = [0,0,…,\frac{\partial a^{l-1} \mathbf{w}_{i:}^l+b^{l}i}{\partial w{ij}^l},..,0] = [0,0,…,a^{l-1}_j,0]$
同理,将$a_j^{l-1}$看作$1$,可得:
$\frac{\partial \mathbf{z}^l}{\partial \mathbf{b}^l} = \mathbf{I}_m$
再令,$ \frac{\partial L(y,\hat{y})}{\partial \mathbf{z}^l } = \mathbf{\delta}^l$,则损失函数对参数z,b求导最后可以写作:
$\frac{\partial L(y,\hat{y})}{\partial w_{ij}^l} = \delta^l_i a_j^{l-1} $
$\frac{\partial L(y,\hat{y})}{\partial \mathbf{b}^l} = \bold{\delta}^l$
Step2: 根据递推公式表示$\bold{\delta}^l$
$\mathbf{z}^{l+1} = \mathbf{W}^{l+1} \mathbf{a}^{l} + \mathbf{b}^{l+1}$
$\mathbf{a}^l = f(\mathbf{z}^l)$
即$\mathbf{z}^l \rightarrow \mathbf{a}^l \rightarrow \mathbf{z}^{l+1}$
$\bold{\delta}^l = \frac{\partial L(y,\hat{y})}{\partial \mathbf{z}^l } = \frac{\partial L(y,\hat{y})}{\partial \mathbf{z}^{l+1} } \frac{\partial \mathbf{z}^{l+1}}{\partial \mathbf{a}^l } \frac{\partial \mathbf{a}^l}{\partial \mathbf{z}^l } = \mathbf{\delta^{l+1}} (\mathbf{W}^{l+1})^T diag(f^{‘}(\mathbf{z}^l)) = f^{‘}(\mathbf{z}^l) \odot \mathbf{\delta^{l+1}} (\mathbf{W}^{l+1})^T$
随机梯度下降训练过程:
输入:训练数据,验证数据
首先 随机初始化参数$\mathbf{W}, \mathbf{b}$
重复以下操作:
对样本随机重排
for n =1 .. N do:
选择一个样本$(\mathbf{x}^n, y^n)$,计算前馈的每一层的净输入$\mathbf{z}^l$和激活值$\mathbf{a}^l$,并计算每一层的误差$\bold{\delta}^l$,这个可以通过step2的公式计算
反向传播,计算每层的偏导,可用step1的公式计算
$\frac{\partial L(y,\hat{y})}{\partial w_{ij}^l} = \delta^l_i a_j^{l-1} $
$\frac{\partial L(y,\hat{y})}{\partial \mathbf{b}^l} = \bold{\delta}^l$
更新参数
$W^l \leftarrow W^l - \alpha\frac{\partial R(W,b)}{\partial W^l} $
$b^l \leftarrow b^l - \alpha\frac{\partial R(W,b)}{\partial b^l} $
end
直至模型在验证集上的错误率不在下降
举例:
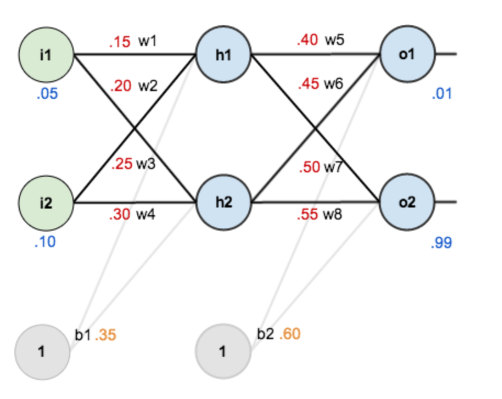
先按传播顺序计算出各个净输入和激活值
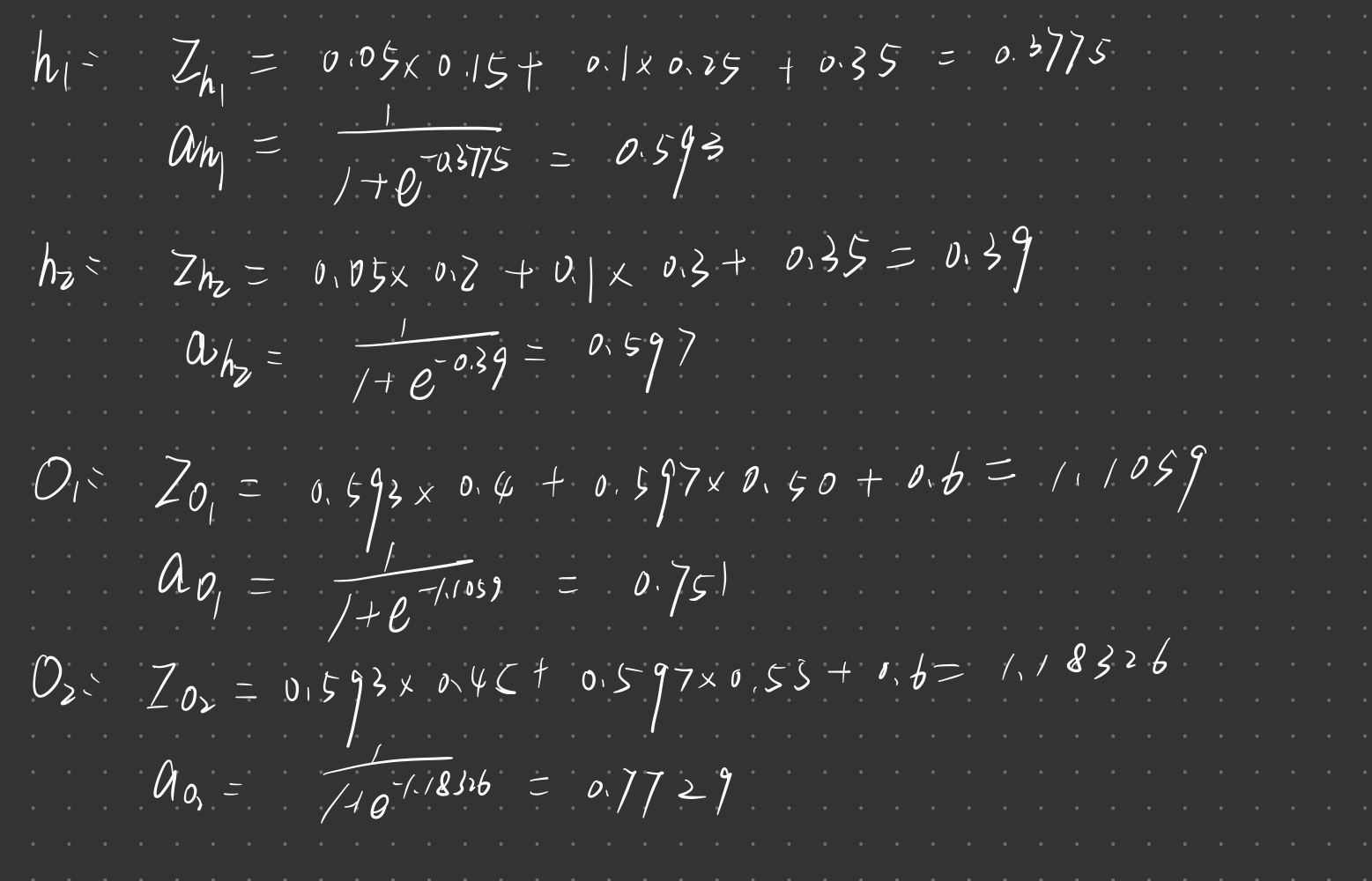
计算输出层
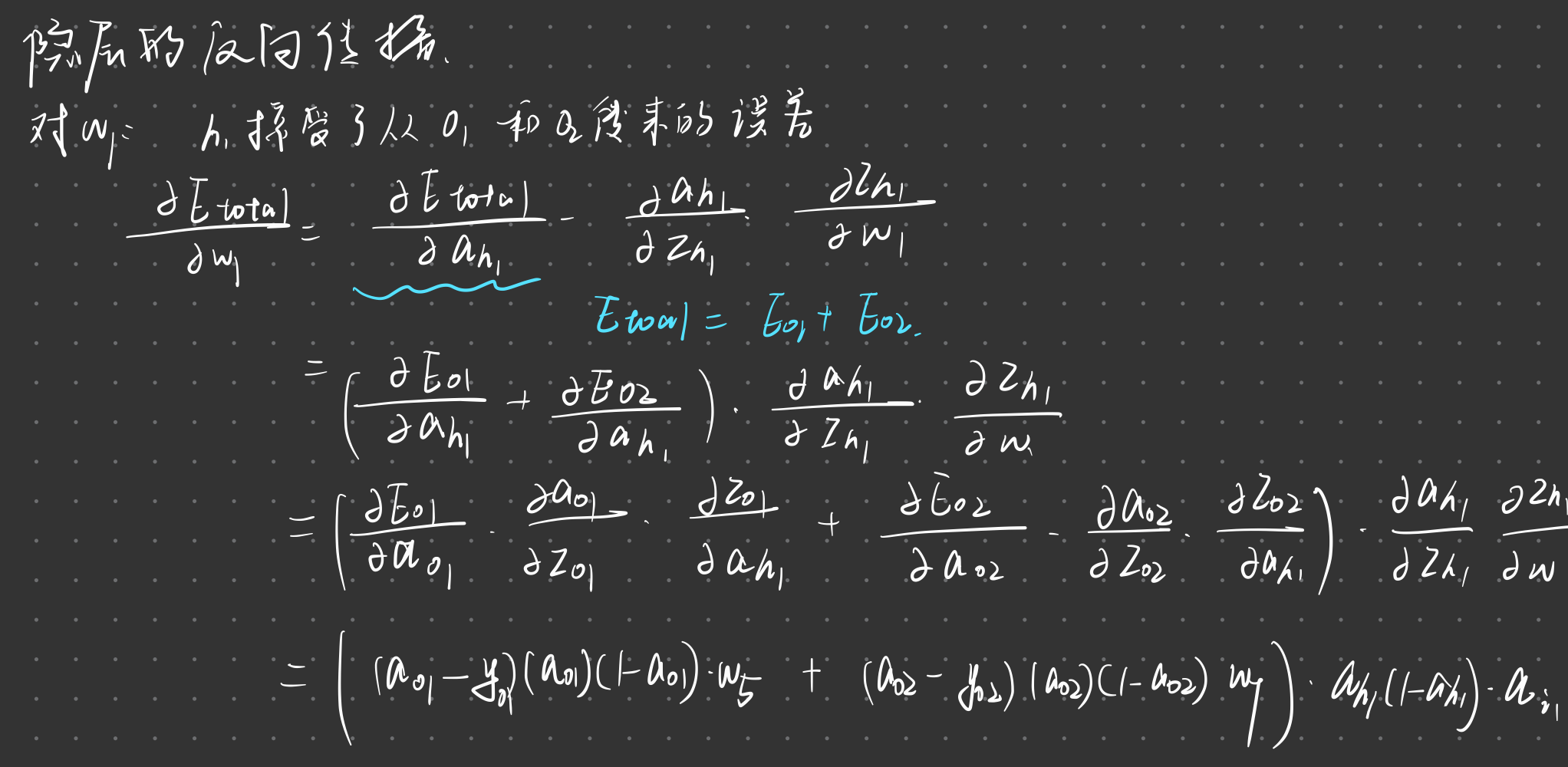
计算这层的误差:$\mathbf{\delta}^l = \hat{y} (1- \hat{y}) (\hat{y} - y)$
更新权值:$\frac{\partial L(y,\hat{y})}{\partial w_{ij}^l} = \delta^l_i a_j^{l-1}$
计算隐藏层
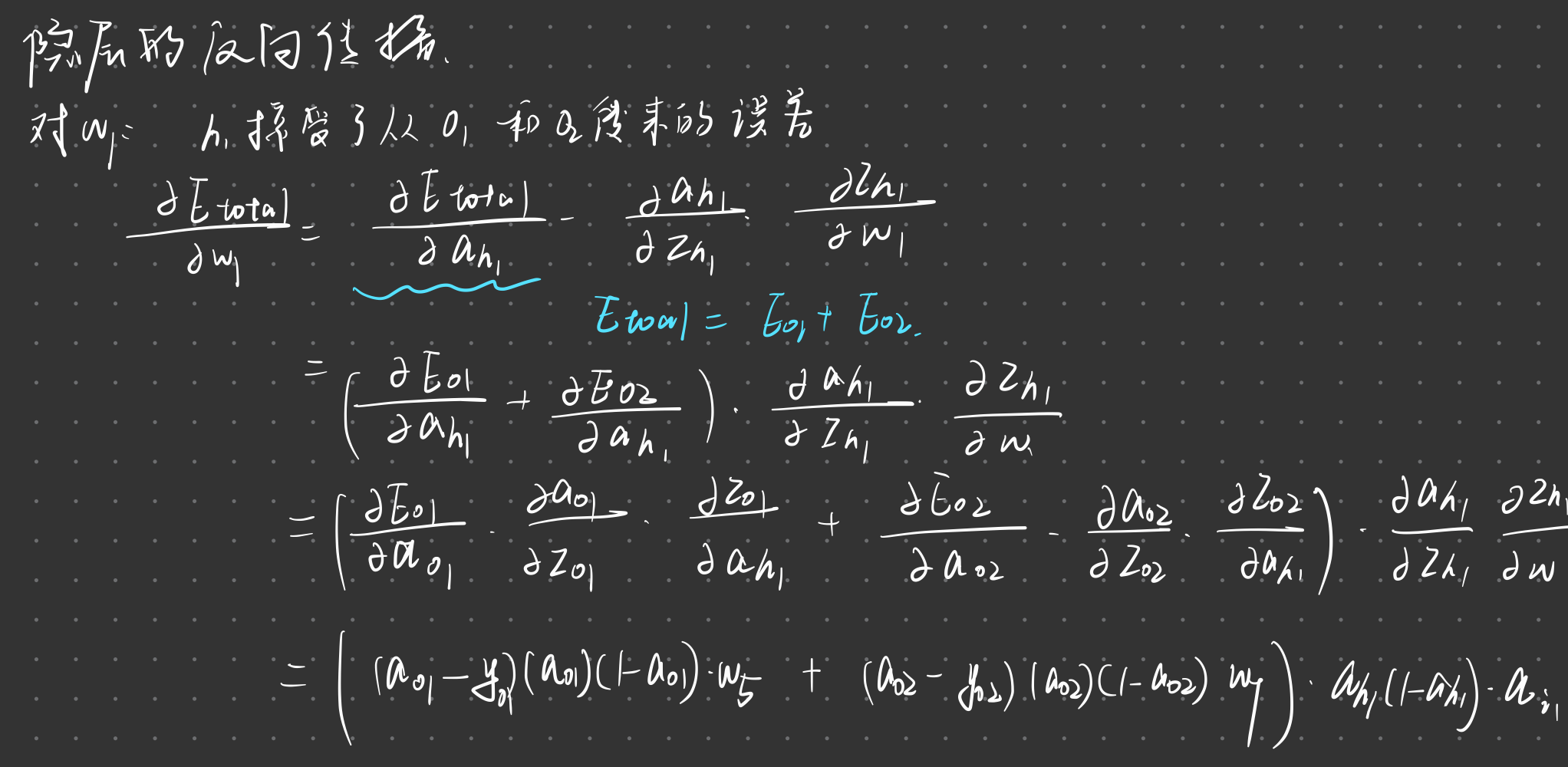
计算这层的误差:$\mathbf{\delta}^l = \hat{y} (1- \hat{y}) \sum(\mathbf{\delta}^{l+1}j)w{ij}$
更新权值:$\frac{\partial L(y,\hat{y})}{\partial w_{ij}^l} = \delta^l_i a_j^{l-1}$
重点
- 前馈神经网络特点
- 激活函数的定义及其导数
- 反向传播算法